Maxim and Increasing Subsequence

题面翻译

给你一个长度为$n$的$B$数组,$A$表示$B$数组复制$t$遍后首尾相连后的数组,求$A$的最长上升子序列 有$k$组询问 $maxb$表示$B$数组中最大的数

题目描述

Maxim loves sequences, especially those that strictly increase. He is wondering, what is the length of the longest increasing subsequence of the given sequence $a$ ?

Sequence $a$ is given as follows:

• the length of the sequence equals $n×t$ ;
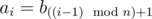• $(1<=i<=n×t)$ , where operation 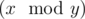means taking the remainder after dividing number $x$ by number $y$ .

Sequence $s_{1},s_{2},...,s_{r}$ of length $r$ is a subsequence of sequence $a_{1},a_{2},...,a_{n}$ , if there is such increasing sequence of indexes $i_{1},i_{2},...,i_{r}$ (1<=i_{1}&lt;i_{2}&lt;...\ &lt;i_{r}<=n) , that $a_{ij}=s_{j}$ . In other words, the subsequence can be obtained from the sequence by crossing out some elements.

Sequence $s_{1},s_{2},...,s_{r}$ is increasing, if the following inequality holds: s_{1}&lt;s_{2}&lt;...&lt;s_{r} .

Maxim have $k$ variants of the sequence $a$ . Help Maxim to determine for each sequence the length of the longest increasing subsequence.

输入格式

The first line contains four integers $k$ , $n$ , $maxb$ and $t$ $ (1<=k<=10; 1<=n,maxb<=10^{5}; 1<=t<=10^{9}; n×maxb<=2·10^{7}) $ . Each of the next $k$ lines contain $n$ integers $b_{1},b_{2},...,b_{n}$ $(1<=b_{i}<=maxb)$ .

Note that for each variant of the sequence $a$ the values $n$ , $maxb$ and $t$ coincide, the only arrays $b$ s differ.

The numbers in the lines are separated by single spaces.

输出格式

Print $k$ integers — the answers for the variants of the sequence $a$ . Print the answers in the order the variants follow in the input.

样例 #1

样例输入 #1

3 3 5 2
3 2 1
1 2 3
2 3 1

样例输出 #1

2
3
3