题目描述

有一个字符串 $S$，它的所有字符都是不超过 $k$ 的正整数 $1,\ldots,k$ 之一。

智者想要知道 $S$ 的具体值，不过尽其一生，他只发现了：

• 有一棵包含 $n$ 个点的以 $1$ 为根的有根树 $T$，已知 $S$ 的后缀字典树与 $T$ 同构。

古书上说：所谓后缀字典树，就是由一个字符串的所有非空后缀生成的字典树。

智者发现：由于 $T$ 的边上并没有标明字符，所以实际上有很多种可能的 $S$，他希望你告诉他满足条件的 $S$ 的数量对 $998244353$ 取模的结果，并构造一种可能的 $S$。

输入格式

第一行：两个整数 $n,k$，分别表示 $T$ 中的点数和 $S$ 的字符集大小。

第二行：$n-1$ 个整数 $f_2,\ldots,f_n$，其中 $f_i$ 表示 $T$ 中点 $i$ 的父结点。

输出格式

第一行：一个整数 $ans$，表示满足条件的 $S$ 的数量对 $998244353$ 取模的结果。

第二行：一个整数 $m$，表示你构造的 $S$ 的长度。

第三行：$m$ 个 $[1,k]$ 中的整数，表示你构造的 $S$。

如果不存在满足条件的 $S$，则只需在第一行输出 $0$，后面不用输出。

样例 1 输入

8 2
1 2 3 1 5 6 7

样例 1 输出

4
4
1 2 1 2

样例 1 解释

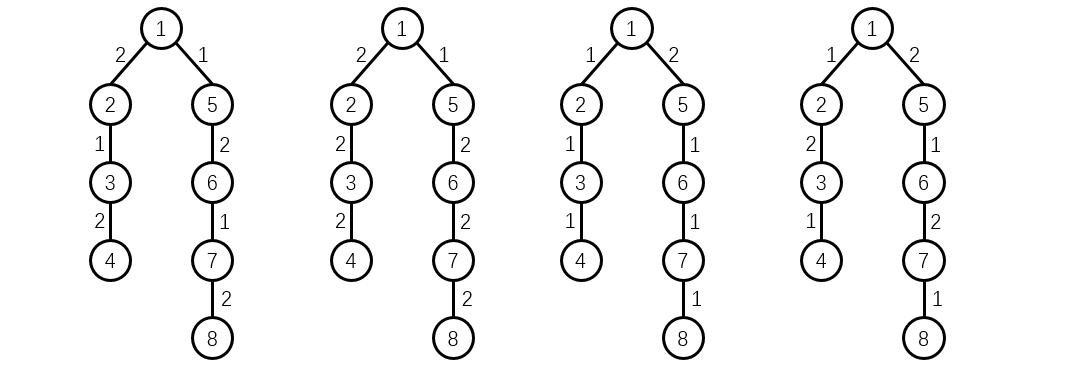
共有 $1\ 2\ 1\ 2,\ 1\ 2\ 2\ 2,\ 2\ 1\ 1\ 1,\ 2\ 1\ 2\ 1$ 这四种可能的 $S$，对应的后缀字典树分别如下图所示：

样例 2 输入

8 2
1 1 2 3 5 5 7

样例 2 输出

0

样例 3 输入

6 4
1 2 3 4 5

样例 3 输出

4
5
3 3 3 3 3

数据范围

对于全部数据：$1\leq n\leq 5\times 10^5,\ 1\leq k\leq 998244352,\ f_i<i$。

子任务编号	$n\leq$	$k\leq$	特殊性质	分值
Subtask 1	$5$	$2$	无	$10$
Subtask 2	$600$		保证有解	$15$
Subtask 3	$2500$	$998244352$
Subtask 4	$5\times 10^5$	$2$	无	$30$
Subtask 5		$998244352$

注：保证有解指的是一定存在满足要求的 $S$。