Statement

众所周知，$\texttt{x}{\color{red}\texttt{yr2005}}$ 是个人赢，有 $5\times 10^5$ 个妹子，但作为一个超强的 OIer，他怎可能只有妹子呢？他不仅有很多毒瘤的数数题，还有很多图。现在 $\texttt{x}{\color{red}\texttt{yr2005}}$ 想给每个妹子整一张图，如果有两个妹子的图比较像，那么她们就会有矛盾，为了维护世界和平，忙着出毒瘤数数题的 $\texttt{x}{\color{red}\texttt{yr2005}}$ 决定找你帮忙。

定义两张无向简单图 $G,H$ 是长得比较像的，当且仅当两者的点集 $V_G,V_H$ 大小相同，且存在一个双射 $\varphi:V_G\rightarrow V_H$，满足若 $G$ 中存在一条边 $uv$，则 $H$ 中存在一条边 $\varphi(u)\varphi(v)$。

对于一张无向联通简单图 $G$ 中的一个顶点 $u$，定义顶点 $u$ 的度数 $\operatorname{deg}(u)$ 为 $G$ 中以 $u$ 为一个顶点的边数。考虑可重集 $D_{u,i}(i\in[0,n-1])=\{\operatorname{deg}(v)|\operatorname{dist}(u,v)=i\}$，其中 $\operatorname{dist}(u,v)$ 表示图 $G$ 中 $u,v$ 之间的最短路长度。定义顶点 $u$ 的度分布 $D_u=[D_{u,0},D_{u,1},...,D_{u,n-1}]$，注意这是列表而不是可重集，即顺序有关。定义图 $G$ 的距离-度分布 为可重集 $P_G=\{D_1,D_2,...,D_n\}$。

例如下图的距离-度分布为 $\{[\{1\},\{2\},\{1\}],[\{2\},\{1,1\},\varnothing],[\{1\},\{2\},\{1\}]\}$。

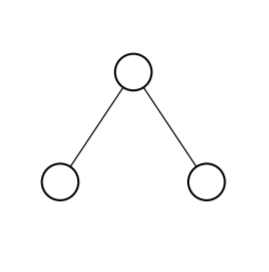
虽然距离-度分布是判定图像不像的一个很强的性质，但若两个图满足距离-度分布相同，他们并不一定长得比较像，例如下图，两者的二度点的度分布均为 $[\{2\},\{3,3\},\{3,3\},\{2\},\varnothing,\varnothing]$，三度点的度分布均为 $[\{3\},\{2,3,3\},\{2,3\},\varnothing,\varnothing,\varnothing]$，但显然两张图不像。

上面的两张图中存在很多度分布完全相同的点，这大大削弱了两张图距离-度分布相同的性质，现在强强的 $\texttt{x}{\color{red}\texttt{yr2005}}$ 有一个猜想：**若两张图 $G,H$ 满足 $P_G=P_H$ 且对于 $G$ 中的任意两个节点 $u,v$ 满足 $D_u\ne D_v$，$H$ 中的任意两个节点 $u,v$ 满足 $D_u\ne D_v$，**那么 $G,H$ 是长得比较像的。

可是这个结论你看上去并不合理，但难以构造反例，为了说明你是比 $\texttt{x}{\color{red}\texttt{yr2005}}$ 更强~~（更赢）的 OIer（人生赢家）~~，你想对于每一个 $n$ 找到图节点数是 $n$ 的反例。但由于距离-度分布相同确实是一个很强的性质，对于一部分 $n$ 可能并没有对应的反例，你只需要报告无解即可。

Input

一行一个整数 $n(1\le n\le 100)$。

Output

第一行一个字符串 YES 或 NO，表示是否存在对应的反例。

若输出是 YES，剩下的输出分成两部分，分别表示你构造的图 $G$ 和 $H$，对于任意一部分：第一行一个正整数 $m$ 表示图的边数，然后 $m$ 行每行两个整数 $u,v$ 表示一条 $u,v$ 之间的边。

因为图是简单图，容易发现 $m\le \frac{n\times (n-1)}{2}$。

你需要保证 $G,H$ 长得不像，$P_G=P_H$，且 $G,H$ 分别满足其中任意两个点 $u,v$ $D_u\ne D_v$。

若输出是 NO，你什么不用多做。

Sample

注意样例只为了方便你理解输入输出格式，他的输出是错的。

input：

4

output

YES
4
1 2
2 3
1 3
1 4
4
1 3
2 3
1 4
2 4

Subtasks

subtask1:$n\le7,40 \text{pts}$

subtask2:$n\le 10,20 \text{pts}$

subtask3:无特殊限制，$40\text{pts}$

Hint

你的坚持，没有错。