#P10848. [POI2021 R2]Agenci
[POI2021 R2]Agenci
题目描述
有一个 个城市的国家,我们可以将其看为一棵 条道路连接的树,有一天,你突发奇想,想要派出 个人在不同城市上。人及其移动需要满足如下条件:
-
每天只能是一个人移动,移动到其相邻存在道路连接一个城市。
-
假如有两个人 ,城市 被 到达过了,则 不能到达 城市。
初始时你知道了人的位置,每个人初始所在地不相同,且该城市视为“已到达过”的城市,你需要安排一个合法的经过城市的方案。
请你求出最少要几天才能使所有的城市都被人到达过。
输入格式
第一行两个整数 $n,k\ (1 \leq n \leq 5 \times 10^5, 1 \leq k \leq n)$。
第二行 个数,表示那些人的初始位置。
然后 行,描述了每条道路 。
输出格式
输出最少天数。
输入输出样例 #1
输入 #1
6 2
2 6
1 2
2 3
2 4
5 4
5 6
输出 #1
5
说明/提示
样例解释:
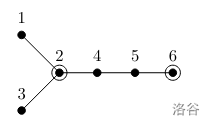
子任务分配如下:
| 子任务编号 | 特殊性质 | 分值 |
|---|---|---|
| 输入为一条链 | ||
| 无特殊性质 |
子任务 为样例。
const int N=5e5+5;
int n,k;
vector<int> e[N];
bool vis[N];
int f[N][2][2];
/*
向上或者向下 单边或者双边
f[u][0][0]:向上的单边
if(!vis[u]){
f[v][0][0]+1+(f[other][1][1]+2)/(f[other][0][0])/(f[other][0][1])
}
else{
(f[son][1][1]+2)/(f[son][0][0])/(f[son][0][1])
}
f[u][0][1]:向上的双边
if(!vis[u]){
f[v][0][1]+2+(f[other][1][1]+2)/(f[other][0][0])/(f[other][0][1])
f[v][0][0]+1+(f[other][1][1]+2)/(f[other][0][0])/(f[other][0][1]) 有一个可以是 f[other][1][0]+1
}
else{
(f[son][1][1]+2)/(f[son][0][0])/(f[son][0][1]) 有一个可以是 f[son][1][0]+1
}
f[u][1][0]:向下的单边
if(!vis[u]){
(f[son][1][1]+2)/(f[son][0][0])/(f[son][0][1]) 有一个可以是 f[son][1][0]+1
}
else{
nope
}
f[u][1][1]:向下的双边
if(!vis[u]){
(f[son][1][1]+2)/(f[son][0][0])/(f[son][0][1])
}
else{
nope
}
*/
inline void dfs(int u,int fa){
for(int v:e[u]) if(v!=fa) dfs(v,u);
if(vis[u]){
for(int v:e[u]) if(v!=fa) f[u][0][0]+=min(f[v][1][1]+2,min(f[v][0][0],f[v][0][1]));
vector<int> g[2];
F(i,0,1) g[i]=vector<int>(e[u].size()+1);
F(i,0,int(e[u].size())-1){
int v=e[u][i],val=min(f[v][1][1]+2,min(f[v][0][0],f[v][0][1]));
if(v!=fa){
g[0][i+1]=g[0][i]+val;
g[1][i+1]=min(g[1][i]+val,g[0][i]+min(val,f[v][1][0]+1));
}else g[0][i+1]=g[0][i],g[1][i+1]=g[1][i];
}
f[u][0][1]=g[1].back();
f[u][1][0]=f[u][1][1]=1e9;
}else{
vector<int> g[4];
F(i,0,1) g[i]=vector<int>(e[u].size()+1);
g[1][0]=1e9;
F(i,0,int(e[u].size())-1){
int v=e[u][i],val=min(f[v][1][1]+2,min(f[v][0][0],f[v][0][1]));
if(v!=fa){
g[0][i+1]=g[0][i]+val;
g[1][i+1]=min(g[1][i]+val,g[0][i]+f[v][0][0]+1);
}else g[0][i+1]=g[0][i],g[1][i+1]=g[1][i];
}
f[u][0][0]=g[1].back();
F(i,0,1) g[i]=vector<int>(e[u].size()+1);
g[1][0]=1e9;
F(i,0,int(e[u].size())-1){
int v=e[u][i],val=min(f[v][1][1]+2,min(f[v][0][0],f[v][0][1]));
if(v!=fa){
g[0][i+1]=g[0][i]+val;
g[1][i+1]=min(g[1][i]+val,g[0][i]+f[v][0][1]+2);
}else g[0][i+1]=g[0][i],g[1][i+1]=g[1][i];
}
f[u][0][1]=g[1].back();
F(i,0,3) g[i]=vector<int>(e[u].size()+1);
g[1][0]=g[3][0]=1e9;
F(i,0,int(e[u].size())-1){
int v=e[u][i],val=min(f[v][1][1]+2,min(f[v][0][0],f[v][0][1]));
if(v!=fa){
g[0][i+1]=g[0][i]+val;
g[1][i+1]=min(g[1][i]+val,g[0][i]+f[v][0][0]+1);
g[2][i+1]=min(g[2][i]+val,g[0][i]+min(val,f[v][1][0]+1));
g[3][i+1]=min(g[3][i]+val,min(g[1][i]+min(val,f[v][1][0]+1),g[2][i]+f[v][0][0]+1));
}else g[0][i+1]=g[0][i],g[1][i+1]=g[1][i],g[2][i+1]=g[2][i],g[3][i+1]=g[3][i];
}
f[u][0][1]=min(f[u][0][1],g[3].back());
F(i,0,1) g[i]=vector<int>(e[u].size()+1);
F(i,0,int(e[u].size())-1){
int v=e[u][i],val=min(f[v][1][1]+2,min(f[v][0][0],f[v][0][1]));
if(v!=fa){
g[0][i+1]=g[0][i]+val;
g[1][i+1]=min(g[1][i]+val,g[0][i]+min(val,f[v][1][0]+1));
}else g[0][i+1]=g[0][i],g[1][i+1]=g[1][i];
}
f[u][1][0]=g[1].back();
for(int v:e[u]) if(v!=fa) f[u][1][1]+=min(f[v][1][1]+2,min(f[v][0][0],f[v][0][1]));
}
// cout<<u<<' '<<f[u][0][0]<<' '<<f[u][0][1]<<' '<<f[u][1][0]<<' '<<f[u][1][1]<<'\n';
}
bool M2;
int main(){
int Time=clock();
look_memory;
cin.tie(nullptr)->sync_with_stdio(false);
cin>>n>>k;
F(i,1,k){
int x;cin>>x;
vis[x]=1;
}
F(i,1,n-1){
int u,v;cin>>u>>v;
e[u].emplace_back(v);
e[v].emplace_back(u);
}
dfs(1,0);
cout<<min(f[1][0][0],f[1][0][1])<<'\n';
look_time;
return 0;
}
