#P11163. [OOI 2025] Strong Connectivity Strikes
[OOI 2025] Strong Connectivity Strikes
题目描述
Vertices and of a directed graph are called strongly connected if there exists a path from to and a path from to in the graph. Note that if and are strongly connected, and and are strongly connected, then and are also strongly connected. Therefore, the vertices of the graph are divided into sets---strongly connected components. A vertex belonging to a strongly connected component is strongly connected to all vertices in the component (including itself) and is not strongly connected to any vertices outside the component.
During a graph class, Alice drew a directed graph with vertices on the board and highlighted its strongly connected components. During the break, Bob decided to play a trick on Alice and erase the directions on some edges of the graph. He wants Alice to be able to uniquely restore the erased directions based on the remaining edges and the partition into strongly connected components after the break.
Help Bob by determining the maximum number of edges in the graph whose directions he can erase, as well as the number of ways he can do this.
More formally, find the maximum size of a subset of edges that has the following property: if the directions of the edges in the set are erased, then based on the information about the old strongly connected components and the directions of the edges not in the set , the directions of the edges in the set can be uniquely restored in such a way that the strongly connected components remain unchanged.
Since the number of such maximum subsets can be very large, output it modulo .
Solutions that correctly determine the maximum size of the set but incorrectly present the number of such subsets will receive partial points.
输入格式
The first line contains three integers , , and (, , )---the number of vertices and edges in the graph, respectively, as well as the test group number.
The next lines contain two integers and (, )---the numbers of the vertices that are the start and end of the -th edge.
It is guaranteed that for any and , meaning that any two vertices are connected by at most one edge, regardless of direction.
输出格式
In the first line, output a single number---the size of the maximum subset of edges whose directions can be erased.
In the second line, output a single number---the number of such subsets modulo . If you do not want to present the number of such subsets, then in the second line, instead, output any number from to . In this case, your solution will receive partial points for the test.
Note that omitting any number in the second line leads to a verdict of "Wrong Answer" and zero points for this test, regardless of the correctness of the size of the subset.
输入输出样例 #1
输入 #1
5 6 0
1 2
1 5
2 3
3 4
3 5
4 2
输出 #1
3
3
说明/提示
Note
The graph from the example with strongly connected components highlighted:
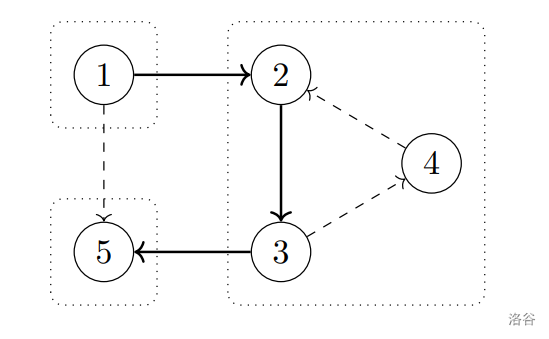
The directions on the dashed edges can be removed. Indeed, the edge cannot be oriented in the opposite direction, because otherwise, vertices , , , and would belong to the same strongly connected component. The edges and cannot be oriented differently either, because then vertices , , and would not belong to the same strongly connected component.
Now, let's consider an incorrect way of selecting a subset of edges:
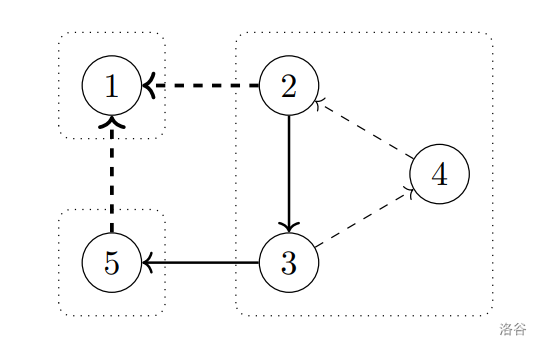
Here, the directions on the bold dashed edges cannot be removed. For example, if we reverse the orientation of edges and , we get a graph with the same decomposition into strongly connected components.
It can be shown that the directions on exactly edges cannot be removed, so the answer is .
Scoring
The tests for this problem consist of seven groups. The rules for scoring the subgroups are described below.
If the size of the maximum subset of edges whose directions can be erased and the number of such subsets are correctly calculated in all tests of the group, full points are awarded for the group.
Otherwise, if the size of the maximum subset of edges whose directions can be erased is correctly calculated in all tests of the group, but the number is incorrect in at least one test of the group, partial points are awarded for the group. Note that dependent groups will be tested in this case and may even be scored full points.
| Group | Partial Points | Full Points | Additional Constraints: | Additional Constraints: | Required Groups | Comment |
|---|---|---|---|---|---|---|
| 0 | -- | Examples. | ||||
| 1 | 7 | 11 | 0 | |||
| 2 | 5 | 9 | 0, 1 | |||
| 3 | 8 | 12 | -- | -- | , for all there is an edge | |
| 4 | 13 | 3 | 。 | |||
| 5 | 12 | 20 | -- | for all there is an edge , there is an edge | ||
| 6 | 13 | 21 | 5 | the graph consists of one strongly connected component | ||
| 7 | 8 | 14 | 0 -- 6 | |||
