Description

三角形网格由边长为 1 的等边三角形组成（参见图 1.3 ）。三角形网格中的路径是网格的任意有限三角形序列（边长为 1），使得每两个连续的三角形共享一条边。

由任意有限数量的三角形的点形成的形状如果包含在该形状中的网格的任何两个三角形通过由该形状中包含的三角形形成的某些路径连接，则称为岛。

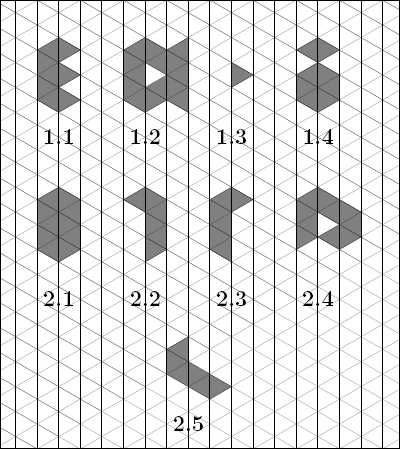
图 1.1、1.2 和 1.3 中的形状是岛。

图 1.4 中的形状不是一个岛。

图 2.2、2.3 和 2.5 中的形状是一致的。

我们的目标是为每个 获得可由边长为 1的三角形形成的所有非全等岛的系统描述，并计算有多少这样的岛。

最多由十个三角形形成的每个岛的边界是由网格的单一部分组成的多边形链。它可以旋转，即

它可以在不从纸上取下铅笔的情况下进行轮廓绘制，这样它的每个部分都被跟踪一次，然后我们回到初始点。尽管某些点必须多次穿过，但可能会发生这种情况（见图 2.4）。

幸运的是，在最多由 10 个三角形形成的岛的情况下，形状的周长是相连的（因此可以在不从纸上拆下铅笔的情况下绘制轮廓），这与图 1.2 中的不同。

在围绕周边盘旋时，在每个单元段之后，我们转动以下任一类型：

a - 向左 120 度，b - 向左 60 度，c - 0 度（即实际上没有转弯），d - 向右 60 度，e - 向右 120 度。

围绕小岛的每个循环都可以用一个单词来描述，该单词由集合中的字母组成，其中每个字母表示在周长组成的每个连续单元段之后应该进行哪个转弯。循环描述的字母与单元段的数量一样多。这意味着我们还描述了多边形链最后一段之后的转弯，即使不需要唯一确定形状。然而，这个多余的字母非常有助于将围绕形状的循环描述转换为仅在初始点不同的另一种描述。

cdddcddd、dcdddcdd、cbbbcbbb 等词描述了围绕图 2.1 形状的不同循环。

单词 cbeddcde、adcabcbb、abcbbadc 描述了围绕图 2.2 形状的不同循环。

单词 acdabbcb i cddebced 描述了围绕图 2.3 形状的不同循环。

如果形状的内部在围绕某个形状的循环中始终位于右侧，我们称这种循环为顺时针循环。

对于每个岛，可以确定与它一致的所有岛的集合以及这些岛的顺时针循环。

一个岛的代码是这样一个词：

它是围绕某个岛的轮廓顺时针循环的描述，与后者一致，它是满足前一个条件的所有单词中按字典顺序排列的最小的单词。

对于图 2.2 和 2.3 中描绘的岛，它们是全等的，我们考虑了围绕它们中的每一个的所有顺时针循环：

Beddcdec, eddcdecb, ddcdecbe, dcdecbed, cdecbedd, decbeddc, ecbeddcd, cbeddcde and bcedcdde, cedcddeb, edcddebc, dcddebce, cddebced, ddebcedc, debcedcd, ebcedcdd 所以它们的通用代码是：bcedicd 上面最小的单词。

图 2.4 中所描绘的岛的代码是：aadecddcddde。

编写一个程序：

对于一个大小岛的给定代码，生成所有大小岛的代码，这些代码可以通过向后者添加一个三角形来获得，对于给定的整数，生成所有大小岛的代码。

输入格式

在标准输入的第一行给出了一个整数( )，表示查询的数量。

以下每一行都包含某种类型的查询。

类型 1 的查询由字母 K 和一个由最多十个三角形组成的岛的代码组成，由一个空格分隔。

类型 2 的查询由字母 N 和一个整数 ( ) 组成，由单个空格分隔。

输出格式

查询的答案应该打印到标准输出中。

对于类型 1 的查询，可以通过从与给定代码描述的岛全等的岛中添加一个三角形来获得岛的不同代码的数量。

在下一行中，所有这些代码（由单个空格分隔）应按字典顺序打印。

对于类型 2 的查询， 应打印由三角形形成的岛的不同代码的数量。

在下一行中，所有这些代码都应按字典顺序打印

输入数据1

2
K adeccecced
N 5

输出数据1

5
acedccecced addebcecced adebebecced adecbedcced cceccecce
4
aedddde bdecdde bececde ccedcde