题目描述

托伦的斜塔流传着许多神秘的传说。塔楼的墙壁是一个圆形，上面有 $N \geq 3$ 个均匀分布的门（换句话说，这些门构成一个正 $N$ 边形的顶点）。这些门从 $0$ 到 $N-1$ 编号，但编号顺序是随机的。具体细节请参阅评分部分。

其中一个鲜为人知的传说是关于每位新塔楼居民必须完成的一项挑战。挑战的目标是从某个门开始，沿圆形塔壁（顺时针或逆时针）行走，列出所有门的顺序，确保每个门恰好访问一次。

这项挑战必须在无法直接看到塔楼的情况下完成。你可以提出如下形式的问题：「给定三个不同的门 $x, y, z$，$\{x, y\}, \{y, z\},\{z, x\}$ 哪对门的距离最近？」问题的回答会列出 $\{x, y\}, \{y, z\}, \{z, x\}$ 中欧几里得距离最小的所有门对。距离是指连接两门的最短线段长度。你的任务是编写一个程序，通过尽量少地提出此类问题，确定门的顺序。

交互方式

这是一个交互题。你需要编写一个程序，通过从标准输入输出与交互器进行交互，找到正确的门的顺序。

交互开始时，你的程序应从标准输入读取两个整数 $t$ 和 $k$ $(1 \leq t \leq 100, 1 \leq k \leq 12000)$，分别表示测试数据组数和允许的平均最大询问次数。关于后者的更多信息，请参阅评分部分。

对于每组测试数据，你的程序应首先从标准输入读取一个整数 $n$ $(3 \leq n \leq 500)$，表示塔楼门的数量。

随后，你的程序应按以下方式提出问题：

• 程序向标准输出输出一行，格式为：

  $\texttt{?}\ x\ y\ z$

  其中 $x, y, z$ $(0 \leq x, y, z \leq n-1)$ 是不同的整数，表示关于门 $x, y, z$ 的一个问题。

• 交互器将返回如下格式的响应：

  $ \begin{aligned} &r \\ &a_1\ b_1 \\ &\ldots \\ &a_r\ b_r \end{aligned} $

  其中 $r$ $(1 \leq r \leq 3)$ 是一个整数，表示距离最小的门对数量。每个门对由两个整数 $a_i$ 和 $b_i$ $(a_i, b_i \in \{x, y, z\}, a_i < b_i)$ 描述。

当你确定门的顺序后，应向标准输出输出一行，格式为：

$\texttt{!}\ x_0\ x_1\ \ldots\ x_{n-1}$

其中 $x_0, x_1, \ldots, x_{n-1}$ 是任务描述中的门的顺序。请注意，由于可以从任意门开始并选择任一方向，总共有 $2n$ 种可能的正确答案，任何一种都会被接受。

请记住，每次询问或回答后，你必须刷新输出缓冲区，例如在 C++ 中使用 cout.flush()（或 fflush(stdout) 如果使用 printf），在 Python 中使用 sys.stdout.flush()。否则，你的程序可能被判定为超时。

在向交互器输出答案后，你的程序应立即处理下一组测试数据，或在所有测试数据处理完毕后结束交互。

你的程序不能打开任何文件或使用其他资源。可以将标准错误流用于调试，但请注意输出此流会耗费时间。

另外，请注意交互器是非自适应的，即每组测试数据中门的初始顺序在交互开始前已固定，不会因交互而改变。

样例

假设只有一组测试数据，$n=6$，门的顺序为 $5, 3, 0, 2, 1, 4$。交互可能如下：

交互器	你的程序	说明
1 100		$t=1$，$k=100$。
6		交互器给出第一组测试数据的门数量。
	? 0 1 2	你的程序询问哪对门距离最近。
2 0 2 1 2		门对 $\{0, 2\}$ 和 $\{1, 2\}$ 距离最近。
	? 4 1 3	你的程序询问哪对门距离最近。
1 1 4		门对 $\{1, 4\}$ 距离最近。
	? 0 5 1	你的程序询问哪对门距离最近。
3 0 5 0 1 1 5		门对 $\{0, 5\}, \{0, 1\}, \{1, 5\}$ 距离最近。
	! 4 5 3 0 2 1	你的程序正确输出门的顺序。

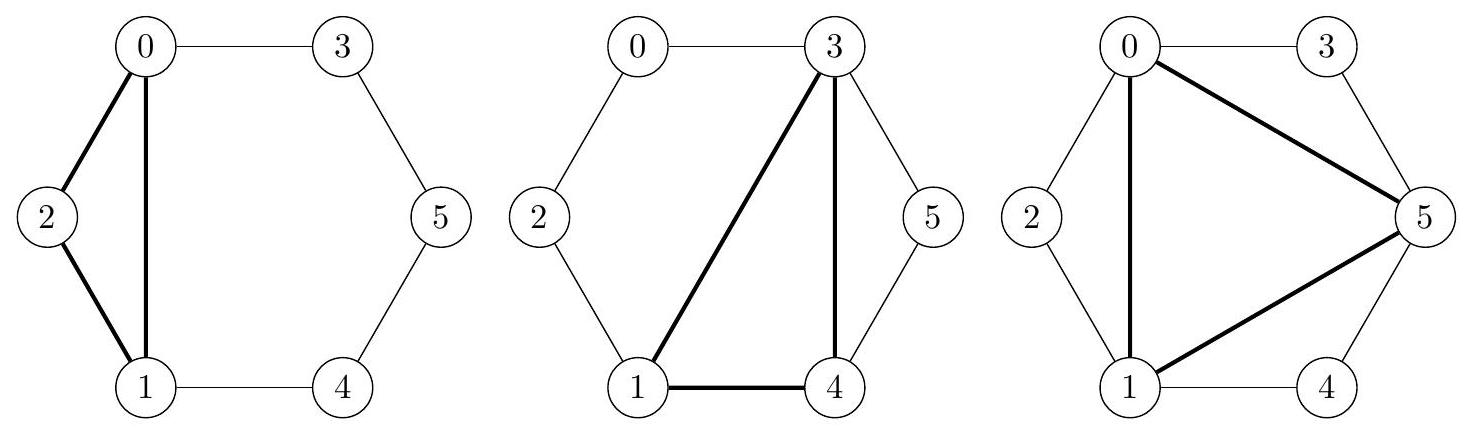
上方的图示展示了塔楼墙壁上的门及其编号。左侧第一幅图显示了编号为 $0, 1, 2$ 的门构成的三角形，对应你的程序的第一次询问，可以看到 $\{0, 2\}$ 和 $\{1, 2\}$ 是距离最近的门对。中间图显示了编号为 $1, 4, 3$ 的门构成的三角形，对应第二次询问，显然 $\{1, 4\}$ 是最近的门对。左侧第三幅图显示了编号为 $0, 1, 5$ 的门构成的三角形，对应第三次询问，所有门对的距离相等。

请注意，在此情况下，序列 $0, 2, 1, 4, 5, 3$ 或 $5, 4, 1, 2, 0, 3$（以及其他几种）也是正确答案。

数据范围与提示

本题的评分分为若干子任务。每个子任务包含正好一个测试，且该测试包含正好 $t=100$ 组测试数据。对于每个测试点，你的程序的平均询问次数通过以下方式计算：将所有测试数据的询问总数除以测试数据数量。如果该平均值对于某个子任务大于 $k$，你将在该子任务中得 $0$ 分。否则，对于子任务 $1$ 到 $4$，你将获得该子任务的满分。

对于最后一个子任务，你的得分按以下方式计算：令 $k^*$ 为你的程序实际的平均询问次数。得分由以下公式给出：

$$\left\lceil 56 \cdot \min \left(1, \frac{12000 - k^*}{7800}\right) \right\rceil $$

这意味着当 $k^*$ 从 $12000$ 减少到 $4200$ 时，得分从 $0$ 线性增加到 $56$。

请注意，如果你的程序在任何测试数据中给出了错误答案，无论询问次数多少，你将在该子任务中得 $0$ 分。

详细子任务附加限制及分值如下表所示。

子任务编号	附加限制	分值
$1$	$k=8000, 3 \leq n \leq 9$	$6$
$2$	$k=4500, 40 \leq n \leq 50$	$7$
$3$	$k=3000, 90 \leq n \leq 100$	$9$
$4$	$k=4500, n=400$，存在一个正确答案 $x_0, \ldots, x_{n-1}$，其中对于 $200 \leq i \leq 399$，$x_i = i$	$22$
$5$	$k=12000, n=500$	$56$

此外，你可以假设每组测试数据是通过以下方式生成的：首先在满足给定子任务限制的所有 $n$ 值中均匀随机选择 $n$，然后在满足子任务限制的所有 $n$ 门顺序中均匀随机选择门的顺序。