题目背景

请注意，你不需要也不应该实现 main 函数。具体实现方式见【实现细节】部分。

题目描述

在一台老旧计算机上使用画图程序。画图程序的屏幕是由称为像素的格子组成的网格。

最左下角的像素坐标为 $(1, 1)$，向右第 $a$ 个、向上第 $b$ 个像素的坐标为 $(a, b)$。初始屏幕上画有 $N$ 个具有垂直和水平边的矩形。矩形由该区域内包含的像素表示。

将对 $N$ 个矩形执行 $M$ 个移动命令。矩形的移动方向包括东、西、南、北四个方向，以及东北、西北、东南、西南（与水平轴成 $45$ 度角）四个方向。此外，移动距离 $d$ 也会给定。换句话说，移动命令由方向和距离组成。具体来说，如果矩形的最左下角像素坐标为 $(a, b)$，那么向东、北、西、南方向移动距离 $d$ 后，其左下角坐标将分别变为 $(a + d, b), (a, b + d), (a - d, b), (a, b - d)$。而向东北、西北、西南、东南方向移动距离 $d$ 后，其左下角坐标将分别变为 $(a + d, b + d), (a - d, b + d), (a - d, b - d), (a + d, b - d)$（见图 1）。

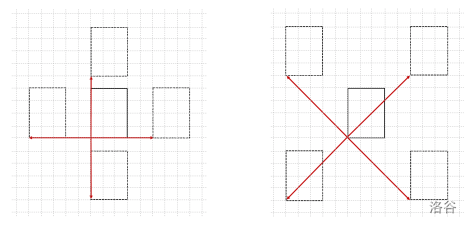
屏幕上矩形 $R$ 的移动距离 $d$ 是通过依次在每移动距离 $1$ 时快速显示 $R$ 的位置来实现的。但由于计算机过于老旧，$R$ 移动时会出现严重的卡顿。因此，$R$ 移动过程中绘制的所有样子都会保留在屏幕上。也就是说，$R$ 移动距离 $d$ 后，屏幕上会新增 $d$ 个矩形。例如，在图 2 中，矩形向东北方向移动距离 $3$ 后，会新增 $3$ 个矩形，最终屏幕上共有 $4$ 个矩形。移动结束后，$R$ 将位于东北方向的终点。

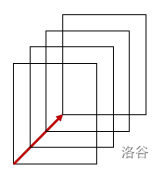
执行完 $M$ 个移动命令后，将给出 $Q$ 个查询。每个查询给出平面上的一个像素 $p$。对于每个查询，需要输出包含像素 $p$ 的矩形数量。

实现细节

你需要实现以下函数：

vector<long long int> count_enclosing_rectangle(vector< pair<int, int> > R1, vector< pair<int, int> > R2, vector<int> V, vector<int> I, vector<int> D, vector< pair<int, int> > P )

• 该函数仅被调用一次。
• 参数数组 R1 和 R2 的大小为 $N$。数组的每个元素表示初始给定的 $N$ 个矩形中的一个，R1[i] 和 R2[i] 分别表示矩形 $i + 1$ 的最左下角和最右上角像素的坐标。坐标以 $(a, b)$ 的形式给出，表示位置为 $(a, b)$。矩形编号为 $1$ 到 $N$ 的整数。
• 参数数组 V、I、D 的大小为 $M$。数组的每个元素表示 $M$ 个矩形移动中的一个，表示矩形 I[i] 向方向 V[i] 移动距离 D[i]。
• 参数数组 P 的大小为 $Q$。数组 P 的每个元素表示查询对应的平面上的像素 $p$ 的坐标，以 $(a, b)$ 的形式给出。
• 该函数需要计算每个查询像素 $p$ 被多少个矩形包含，并将结果存储在长度为 $Q$ 的数组中返回。第 $i$ 个值应为第 $i$ 个查询的结果（$0 \leq i \leq Q - 1$）。

提交的源代码中不得调用任何输入输出函数。

输入格式

示例评测程序按以下格式接收输入：

• 第 $1$ 行：$N \ M \ Q$
• 第 $1 + i$ 行（$1 \leq i \leq N$）：$\texttt{R1[i - 1].first R1[i - 1].second R2[i - 1].first R2[i - 1].second}$
• 第 $1 + N + i$ 行（$1 \leq i \leq M$）：$\texttt{V[i - 1] I[i - 1] D[i - 1]}$
• 第 $1 + N + M + i$ 行（$1 \leq i \leq Q$）：$\texttt{P[i - 1].first P[i - 1].second}$

输出格式

示例评测程序输出以下内容：

• 第 $i$ 行（$1 \leq i \leq Q$）：函数 count_enclosing_rectangle 返回数组的第 $i$ 个元素。

请注意，示例评测程序与实际评测程序可能不同。

输入输出样例 #1

输入 #1

3 3 4
1 1 2 2
3 3 4 4
4 1 6 2
1 1 2
6 2 2
2 3 3
3 3
4 3
3 2
5 3

输出 #1

4
5
3
2

说明/提示

约束条件

• $1 \leq N \leq 250,000$
• $0 \leq M \leq 250,000$
• $1 \leq Q \leq 250,000$
• $1 \leq \texttt{R1[i].first} \leq \texttt{R2[i].first} \leq 250,000$
• $1 \leq \texttt{R1[i].second} \leq \texttt{R2[i].second} \leq 250,000$
• $0 \leq \texttt{V[i]} \leq 7$
• $1 \leq \texttt{I[i]} \leq N$
• $1 \leq \texttt{D[i]} \leq 250,000$
• 屏幕上的坐标值在 $1$ 到 $250,000$ 之间。任何矩形包含的所有像素的坐标值始终在此范围内，移动后也满足此条件。查询的像素也满足此条件。
• 矩形移动方向 V[i] 的值为：$0$（东）、$1$（东北）、$2$（北）、$3$（西北）、$4$（西）、$5$（西南）、$6$（南）、$7$（东南）。

子任务

1. （$8$ 分）
   • $N \leq 100$，$M = 0$
2. （$8$ 分）
   • $M = 0$
3. （$11$ 分）
   • $M \leq 100$
4. （$13$ 分）
   • $\text{V}[i] \in \{0, 2, 4, 6\}$（$0 \leq i \leq M - 1$），即矩形仅沿水平或垂直方向移动。
5. （$12$ 分）
   • $\text{R1}[i] = \text{R2}[i]$（$0 \leq i \leq N - 1$）
6. （$48$ 分）
   • 无额外约束条件。

评分标准

只有当 count_enclosing_rectangle 函数返回的数组长度为 $Q$，并且与正确答案数组的所有元素完全一致时，才判定为该测试用例正确。

示例

• $N = 3$，$M = 3$，$Q = 4$，R1 = [(1, 1), (3, 3), (4, 1)]，R2 = [(2, 2), (4, 4), (6, 2)]，V = [1, 6, 2]，I = [1, 2, 3]，D = [2, 2, 3]，P = [(3, 3), (4, 3), (3, 2), (5, 3)]时，考虑以下情况。

  评测程序将调用以下函数：

  count_enclosing_rectangle(R1, R2, V, I, D, P)
  

  在此示例中，$3$ 个矩形的 $3$ 次移动共生成 $7$ 个新矩形，因此最终屏幕上有 $10$ 个矩形。像素 $(3, 3)$ 被矩形 $1$ 生成的 $2$ 个矩形和矩形 $2$ 生成的 $2$ 个矩形包含，因此共被 $4$ 个矩形包含。注意，矩形 $1$ 的第三次移动生成的矩形与矩形 $2$ 的矩形虽然区域相同，但被视为不同的矩形。

  

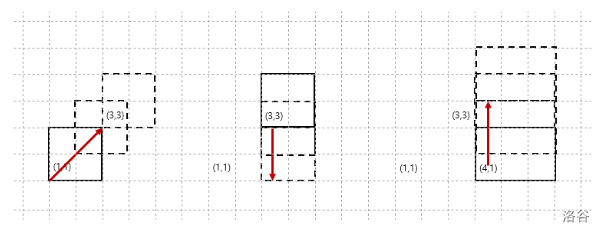
  函数 count_enclosing_rectangle 应返回数组 [4, 5, 3, 2]。