题目描述

对于笛卡尔平面上的两个点 $(x_1, y_1)$ 和 $(x_2, y_2)$，我们定义它们之间的曼哈顿距离为 $|x_1-x_2|+|y_1-y_2|$。例如，点 $(4, 1)$ 和 $(2, 7)$ 之间的曼哈顿距离为 $|4-2|+|1-7| = 2+6 = 8$。

给定笛卡尔平面上的 $2 \cdot n$ 个点，其坐标均为整数。所有给定点的 $y$ 坐标要么是 $0$，要么是 $1$。

将这些点分成 $n$ 对，使得每个点恰好属于一对，并且所有配对中两点之间的最大曼哈顿距离最小化。

输入格式

第一行包含一个整数 $n$ $(1 \le n \le 10^5)$。

接下来的 $2 \cdot n$ 行，每行包含两个整数 $x_i$ 和 $y_i$ $(0 \le x_i \le 10^9, 0 \le y_i \le 1)$ —— 对应点的坐标。

输出格式

输出一个整数 —— 最优配对方案中所有配对两点之间的最大曼哈顿距离。

输入输出样例 #1

输入 #1

1
3 1
1 0

输出 #1

3

输入输出样例 #2

输入 #2

3
18 0
3 0
1 0
10 0
8 0
14 0

输出 #2

4

输入输出样例 #3

输入 #3

4
3 0
0 1
5 0
2 1
6 0
3 0
5 1
2 1

输出 #3

2

说明/提示

在第二个样例中，配对 $[(18, 0), (14, 0)]$、$[(3, 0), (1, 0)]$ 和 $[(8, 0), (10, 0)]$ 是唯一的最优划分方案。该方案中各对点之间的曼哈顿距离分别为 $4$、$2$ 和 $2$。

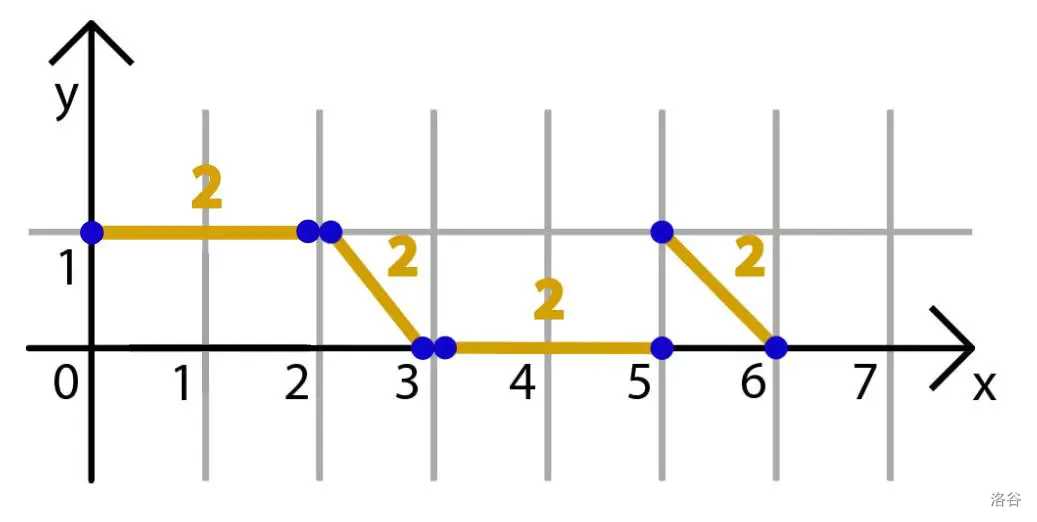
在第三个样例中，配对 $[(0, 1), (2, 1)]$、$[(2, 1), (3, 0)]$、$[(3, 0), (5, 0)]$ 和 $[(5, 1), (6, 0)]$ 是一个最优划分方案。该方案中所有配对两点之间的曼哈顿距离均为 $2$。

第三个样例的图示

评分标准

• （$2$ 分）：$n = 1$；
• （$3$ 分）：对于所有 $1 \le i \le 2\cdot n$，$x_i = 0$；
• （$4$ 分）：$n \le 4$；
• （$11$ 分）：$n \le 10$；
• （$14$ 分）：对于所有 $1 \le i \le 2\cdot n$，$y_i = 0$；
• （$10$ 分）：对于所有 $1 \le i < j \le 2\cdot n$，$x_i \neq x_j$；
• （$29$ 分）：$n \le 1000$；
• （$27$ 分）：无额外限制。