题目描述

简单多边形是指不自交且无洞的多边形。给定一个简单多边形的 $N$ 个顶点 $v_1, v_2, \ldots, v_N$，其中 $v_i = (x_i, y_i)$，$x_i$ 和 $y_i$ 分别是第 $i$ 个顶点的 $x$ 坐标和 $y$ 坐标。顶点互不相同且按逆时针顺序给出（因此每对相邻顶点之间有一条边；$v_N$ 和 $v_1$ 之间也有一条边）。

多边形的边界不经过任何格点（格点是指两个坐标均为整数的点）。此外，所有 $x_i$ 和 $y_i$ 的值均不为整数。

半整数点是指恰好有一个坐标为整数的点。设 $\mathcal{P} = \left\{p_1, p_2, \ldots, p_k\right\}$ 为多边形边界上的所有半整数点。对于每个半整数点 $p_i \in \mathcal{P}$，令 $n_i$ 为 $p_i$ 的非整数坐标的下取整值。对于 $\mathcal{P}$ 的子集 $\mathcal{S}$，定义 $\sigma(\mathcal{S})$ 为 $\mathcal{S}$ 中所有点的 $n_i$ 之和（$\sigma(\emptyset) = 0$）。是否存在一种将 $\mathcal{P}$ 划分为两个子集 $\mathcal{S}_1$ 和 $\mathcal{S}_2$ 的方法，使得 $\sigma(\mathcal{S}_1) = \sigma(\mathcal{S}_2)$？

（两个集合 $\mathcal{S}_1$ 和 $\mathcal{S}_2$ 构成 $\mathcal{P}$ 的划分，当且仅当 $\mathcal{P} = \mathcal{S}_1 \cup \mathcal{S}_2$ 且 $\mathcal{S}_1 \cap \mathcal{S}_2 = \emptyset$。只要满足这两个条件且 $\sigma(\mathcal{S}_1) = \sigma(\mathcal{S}_2)$，对 $\mathcal{S}_1$ 和 $\mathcal{S}_2$ 没有其他限制。特别地，允许空集，且每个子集中的半整数点不必在多边形边界上连续。）

输入格式

第一行输入一个整数 $N$（$3 \leq N \leq 500$），表示多边形的顶点数。

接下来的 $N$ 行，每行包含两个实数 $x_i$ 和 $y_i$（$-500 < x_i, y_i < 500$），表示多边形顶点的坐标，按逆时针顺序给出。每个坐标的小数部分恰好有 $6$ 位，且不为整数。

保证多边形不自交、顶点互不相同，且多边形边界不经过任何格点。

输出格式

如果无解，输出 $-1$ 并结束。

否则，第一行输出一个整数 $M$，表示划分 $\mathcal{P}$ 后其中一个子集中的半整数点数量。接下来的 $M$ 行，每行输出该子集中一个点的 $n_i$ 值。

如果存在多个有效划分，可以任选其一。可以输出划分中的任意一个子集，且 $n_i$ 值可以按任意顺序列出。

输入输出样例 #1

输入 #1

4
-0.950000 -0.850000
-0.100000 0.999999
0.111000 0.555000
-0.200000 1.600000

输出 #1

3
0
-1
-1

输入输出样例 #2

输入 #2

3
0.500000 0.700000
0.100000 0.200000
0.800000 0.900000

输出 #2

0

输入输出样例 #3

输入 #3

4
-360.000001 -24.000001
-359.999999 -24.000001
-359.999999 -23.999999
-360.000001 -23.999999

输出 #3

2
-25
-360

说明/提示

样例输入 1 对应的多边形如下图所示：

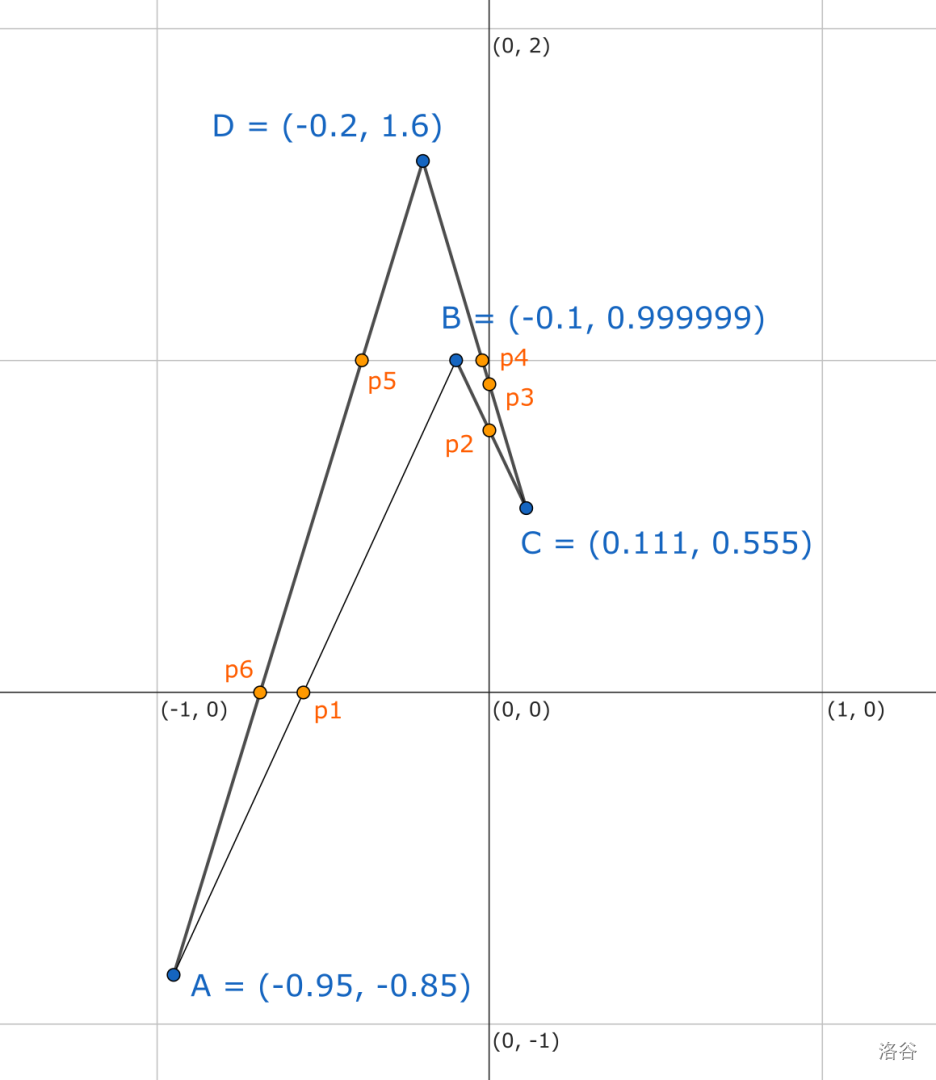
顶点标记为 $A,B,C,D$。半整数点用橙色标出，从 $A$ 开始逆时针依次标记为 $p_i$。这些半整数点的 $n_i$ 值依次为 $-1, 0, 0, -1, -1, -1$。任何 $n_i$ 之和为 $-2$ 的子集均为正确答案。样例输出 1 展示了一种可能的正确答案。

样例输入 2 的多边形边界未经过任何半整数点，因此 $\mathcal{P}$ 为空集，可以划分为两个空集，其 $\sigma$ 值均为零。