题目描述

你的朋友给了你一棵有根树：一个包含 $N$ 个节点和 $N-1$ 条边的连通图。树的节点编号为 $1$ 到 $N$，其中节点 $1$ 是树的根，其他节点的编号是任意的。

然而，你最近了解到衔尾蛇（Ouroboros），一种古老的神话蛇，它咬住自己的尾巴，象征着一个无始无终的循环。你不喜欢这棵树的清晰结构——根是起点，叶子是终点，因此你决定彻底改变这棵树的结构，构建一种新的图，你称之为 衔尾蛇图。

为了构造这个衔尾蛇图，你取出树的所有叶子节点（没有直接子节点的节点），并在每个叶子和根之间添加特殊的“叶子”边。如果某个叶子已经有一条连接到根的边，你仍然会添加一条重复的边。

在这种特殊的图结构下，你可以通过删除某些边的子集来生成许多不同的树。在衔尾蛇的精神下，根和叶子的身份会随着删除的边而变化。问：通过从衔尾蛇图中删除某些边的子集，可以生成多少种不同的树？如果两棵树有一条边存在于其中一棵树但不存在于另一棵树，则认为它们是不同的。（如果一条普通边和一条“叶子”边连接同一对节点，它们被视为不同的边。）由于树的数量可能很大，请将答案对 $998\,244\,353$ 取模。

输入格式

第一行输入包含一个整数 $N$（$2 \leq N \leq 200\,000$），表示树的节点数。

接下来的 $N-1$ 行每行包含两个空格分隔的整数 $a$ 和 $b$（$1 \leq a,b \leq N$），表示树中父节点 $a$ 和子节点 $b$ 之间有一条边。输入保证给定的图是一棵树：图中任意两个节点之间有且仅有一条路径。

输出格式

输出从衔尾蛇图中删除某些边的子集后可以形成的不同树的数量，结果对 $998\,244\,353$ 取模。

输入输出样例 #1

输入 #1

8
1 3
3 2
1 4
1 7
7 6
6 5
6 8

输出 #1

72

说明/提示

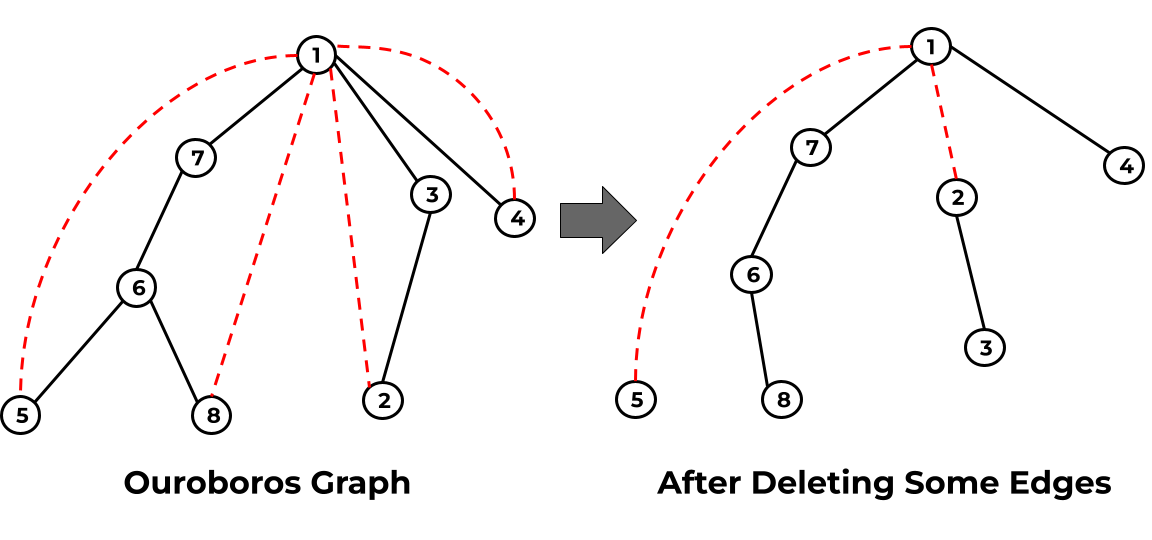
在下面的示意图中，左侧子图展示了样例输入 1 对应的衔尾蛇图，其中原始树边用黑色实线表示，新增的“叶子”边用红色虚线表示。右侧的树展示了从衔尾蛇图中删除某些边后形成的 $72$ 种可能的不同树之一：在这个例子中，原始边 $6$--$5$ 和 $1$--$3$ 以及“叶子”边 $1$--$8$ 和 $1$--$4$ 被删除了。