题目描述

你负责一个铁路网络的维护工作。该网络由 $\mathbf{N}$ 个车站和 $\mathbf{L}$ 条铁路线组成。每条铁路线双向服务于一个固定的车站列表（列车在列表的第一个和最后一个车站调头）。在一个车站可以从一条线路换乘到另一条线路，这意味着从车站 $a$ 到车站 $b$ 的行程是可行的，如果存在一个铁路线列表，其中第一条线路服务于车站 $a$，最后一条线路服务于车站 $b$，并且对于列表中任意两条相邻的铁路线，至少存在一个车站同时被这两条线路服务。

最简单的维护方式是每次关闭整条铁路线。然而，有些铁路线可能是关键线路。一条铁路线是关键线路，如果移除它后会导致至少一对车站之间的行程变得不可能。

给定现有的铁路线列表，计算其中有多少条是关键线路。

输入格式

输入的第一行给出测试用例的数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例以一行包含两个整数 $\mathbf{N}$ 和 $\mathbf{L}$ 开始：分别表示网络中的车站数量和铁路线数量。接着是 $\mathbf{L}$ 组数据，每组包含 2 行。第 $i$ 组的第一行包含一个整数 $\mathbf{K}_i$，表示第 $i$ 条铁路线服务的车站数量。第 $i$ 组的第二行包含 $\mathbf{K}_i$ 个整数 $\mathbf{S}_{i,1}, \mathbf{S}_{i,2}, \ldots, \mathbf{S}_{i,\mathbf{K}_i}$，表示第 $i$ 条铁路线服务的车站。

输出格式

对于每个测试用例，输出一行 Case #x: y，其中 $x$ 是测试用例编号（从 1 开始），$y$ 是关键铁路线的数量。

输入输出样例 #1

输入 #1

4
4 3
3
1 2 3
2
1 4
3
4 1 3
4 4
2
1 2
2
3 4
2
3 2
2
4 1
4 3
2
1 2
2
3 4
2
3 2
4 3
2
1 2
2
3 4
4
4 1 2 3

输出 #1

Case #1: 1
Case #2: 0
Case #3: 3
Case #4: 1

说明/提示

样例解释

在样例 #1 中，第一条铁路线是关键线路，因为它是唯一服务于车站 $2$ 的线路。由于关闭其他任何线路都不会导致至少一对车站之间的行程变得不可能，因此它们不是关键线路。

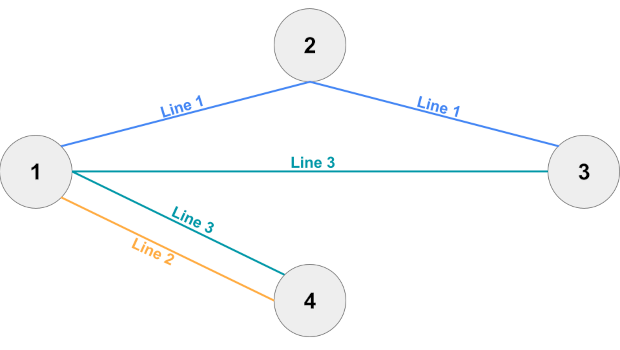
在样例 #2 中，没有关键线路。

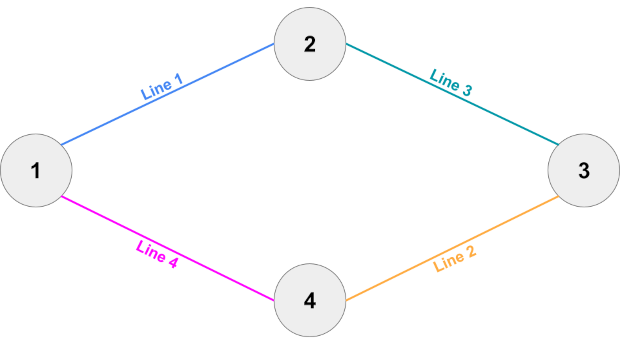
样例 #3 与样例 #2 类似，但缺少最后一条铁路线。这使得剩余的所有铁路线都成为关键线路。

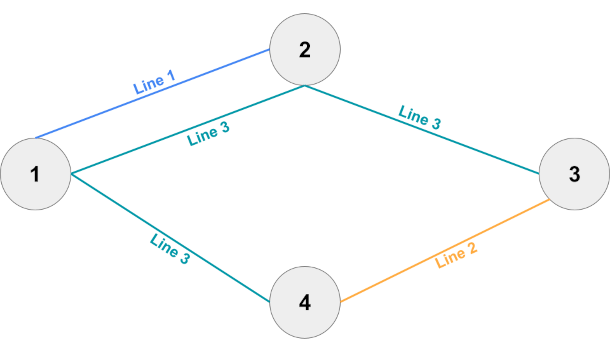
在样例 #4 中，最后一条铁路线是关键线路，因为没有它就无法从车站 $1$ 到达车站 $4$。与样例 #1 类似，由于这条铁路线已经连接了所有车站，其他线路都不是关键线路。

数据范围

• $1 \leq \mathbf{T} \leq 100$。
• 对所有 $i$，$2 \leq \mathbf{K}_i \leq \mathbf{N}$。
• 对所有 $i, j$，$1 \leq \mathbf{S}_{i,j} \leq \mathbf{N}$。
• 对所有 $i, j, j'$ 且 $j \neq j'$，$\mathbf{S}_{i,j} \neq \mathbf{S}_{i,j'}$（每条铁路线中每个车站最多出现一次）。

根据上述定义，当没有铁路线被关闭时，所有车站对之间的行程都是可行的。

测试集 1（9 分，可见判定）

• $2 \leq \mathbf{N} \leq 100$。
• $1 \leq \mathbf{L} \leq 100$。
• $\mathbf{K}_1 + \mathbf{K}_2 + \cdots + \mathbf{K}_\mathbf{L} \leq 200$。

测试集 2（20 分，可见判定）

• $2 \leq \mathbf{N} \leq 10^5$。
• $1 \leq \mathbf{L} \leq 10^5$。
• $\mathbf{K}_1 + \mathbf{K}_2 + \cdots + \mathbf{K}_\mathbf{L} \leq 2 \times 10^5$。