题目描述

今天是你和你的双胞胎兄弟姐妹的生日。为了庆祝，你们得到了一个长方形的蛋糕来分享。蛋糕上装饰有 $\mathbf{N}$ 个三角形的糖霜区域（这些区域可能重叠）。所有的糖霜区域都是用同一个三角形模具制作的，因此它们的形状和方向完全相同。尽管你和你的双胞胎非常相似，但你们对糖霜的喜好却大不相同。具体来说，吃掉第 $i$ 个糖霜区域的全部，你会获得 $\mathbf{A}_i$ 的享受值，而你的双胞胎会获得 $\mathbf{B}_i$ 的享受值。如果有人吃掉了一部分糖霜区域，他们获得的享受值与吃掉的部分面积成正比。例如，如果你吃掉了第 $i$ 个糖霜区域的 $\frac{2}{3}$，你会获得 $\frac{2\mathbf{A}_i}{3}$ 的享受值。注意，有些糖霜口味可能是你或你的双胞胎不喜欢的，因此 $\mathbf{A}_i$ 和/或 $\mathbf{B}_i$ 的值可能是负数。

你将通过一次垂直切割（平行于 Y 轴）将蛋糕分成两个长方形部分。切完蛋糕后，你将吃掉左边的部分，而你的双胞胎将吃掉右边的部分。你的总享受值是你从切割线左侧所有糖霜区域获得的享受值之和。类似地，你的双胞胎的总享受值是他们从切割线右侧所有糖霜区域获得的享受值之和。

为了尽可能公平，你希望切割蛋糕使得你和你的双胞胎的总享受值之差的绝对值尽可能小。给定长方形蛋糕上的 $\mathbf{N}$ 个三角形糖霜区域，你和你的双胞胎的总享受值之差的最小可能绝对值是多少？

输入格式

输入的第一行包含测试用例的数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例的第一行包含三个正整数 $\mathbf{N}$、$\mathbf{W}$ 和 $\mathbf{H}$，分别表示蛋糕上的糖霜区域数量、蛋糕顶部的宽度和高度。蛋糕的左下角位于 $(0,0)$，右上角位于 $(\mathbf{W}, \mathbf{H})$。接下来的一行描述糖霜区域模具，包含四个整数 $\mathbf{P}$、$\mathbf{Q}$、$\mathbf{R}$ 和 $\mathbf{S}$。糖霜区域模具是一个顶点位于 $(0,0)$、$(\mathbf{P}, \mathbf{Q})$ 和 $(\mathbf{R}, \mathbf{S})$ 的三角形。随后是 $\mathbf{N}$ 行，每行包含四个整数 $\mathbf{X}_i$、$\mathbf{Y}_i$、$\mathbf{A}_i$ 和 $\mathbf{B}_i$。第 $i$ 个糖霜区域是一个顶点位于 $(\mathbf{X}_i, \mathbf{Y}_i)$、$(\mathbf{X}_i + \mathbf{P}, \mathbf{Y}_i + \mathbf{Q})$ 和 $(\mathbf{X}_i + \mathbf{R}, \mathbf{Y}_i + \mathbf{S})$ 的三角形。你会从吃掉它中获得 $\mathbf{A}_i$ 的享受值，而你的双胞胎会获得 $\mathbf{B}_i$ 的享受值。

输出格式

对于每个测试用例，输出一行 Case #x: y/z，其中 $x$ 是测试用例编号（从 1 开始），$\frac{y}{z}$ 是通过一次垂直切割可以实现你和你的双胞胎总享受值之差的最小绝对值，且必须为不可约分式（即 $z$ 必须为正且尽可能小）。

输入输出样例 #1

输入 #1

4
1 5 5
3 -1 2 2
1 2 -10 5
2 100000000 50000000
80000000 0 40000000 40000000
5000001 2500000 500 -501
15000000 5000000 501 -400
2 10 10
0 2 4 2
2 2 -4 5
4 6 -6 5
3 622460462 608203753
486076103 36373156 502082214 284367873
98895371 126167607 823055173 -740793281
26430289 116311281 -398612375 -223683435
46950301 278229490 766767410 -550292032

输出 #1

Case #1: 5/1
Case #2: 288309900002019999899/320000000000000000
Case #3: 37/4
Case #4: 216757935773010988373334129808263414106891/187470029508637421883991794137967

说明/提示

样例解释

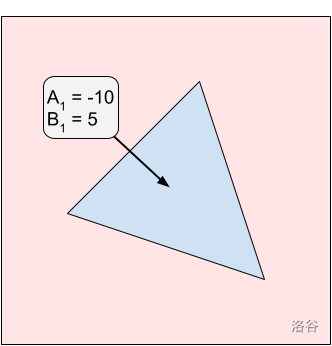
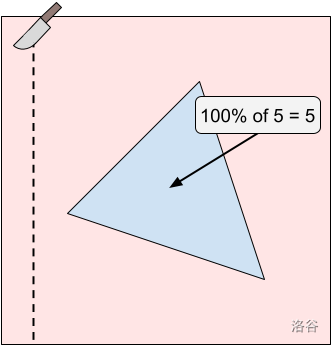
在样例 #1 中，只有一个糖霜区域。最优切割位于该区域的左侧。你将不会吃到任何糖霜，享受值为 0。你的双胞胎会吃掉整个糖霜区域并获得 5 的享受值。你和你的双胞胎享受值之差的绝对值为 $|0 - 5| = 5$。

在样例 #2 中，有两个糖霜区域。最优切割位于 $X = 15099999.99$ 处。注意答案的分子和分母可能非常大。

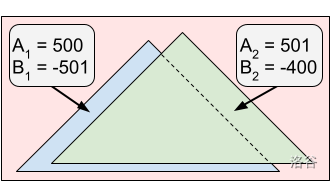
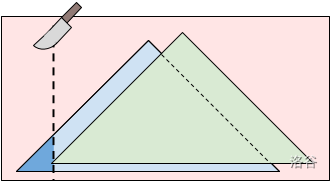
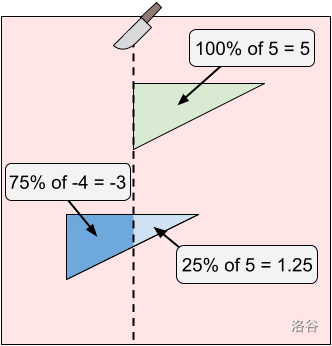
在样例 #3 中，有两个糖霜区域。最优切割位于 $X = 4$ 处。你将吃掉第一个糖霜区域的 75%，获得 $-3$ 的享受值。你的双胞胎会吃掉第一个糖霜区域的 25% 和整个第二个糖霜区域，获得 $5 \times 0.25 + 5 = 6.25$ 的享受值。你和你的双胞胎享受值之差的绝对值为 $|-3 - 6.25| = 9.25 = \frac{37}{4}$。

注意，在 $X = 1$ 处切割会让你获得 $0$ 享受值，而你的双胞胎获得 $10$ 享受值。虽然这两个值都比在 $X = 4$ 处切割时的对应值大，但它们之间的差值为 $10 > 9.25$，因此仍然选择在 $X = 4$ 处切割更优。

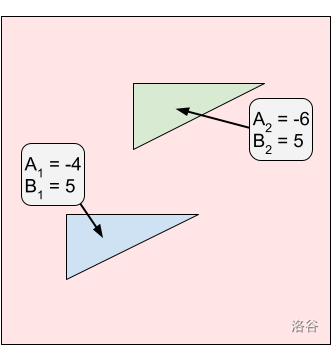
在样例 #4 中，有三个糖霜区域。最优切割位于 $X \approx 521241077.6027$ 处。

测试集 1（20 分，可见判定）

• $1 \leq \mathbf{T} \leq 100$。
• $1 \leq \mathbf{N} \leq 100$。
• $3 \leq \mathbf{W} \leq 10^{9}$。
• $3 \leq \mathbf{H} \leq 10^{9}$。
• $-10^{9} \leq \mathbf{A}_{i} \leq 10^{9}$，对所有 $i$ 成立。
• $-10^{9} \leq \mathbf{B}_{i} \leq 10^{9}$，对所有 $i$ 成立。
• $0 \leq \mathbf{P} \leq 10^{9}$。
• $-10^{9} \leq \mathbf{Q} \leq 10^{9}$。
• $0 \leq \mathbf{R} \leq 10^{9}$。
• $-10^{9} \leq \mathbf{S} \leq 10^{9}$。
• 模具的三个顶点 $(0, 0)$、$(\mathbf{P}, \mathbf{Q})$ 和 $(\mathbf{R}, \mathbf{S})$ 不共线。
• 每个三角形糖霜区域的三个顶点严格位于蛋糕的边界内。即：
  • $1 \leq \mathbf{X}_{i} \leq \mathbf{W} - \max(\mathbf{P}, \mathbf{R}) - 1$，对所有 $i$ 成立；
  • $\max(0, -\mathbf{Q}, -\mathbf{S}) + 1 \leq \mathbf{Y}_{i} \leq \mathbf{H} - \max(0, \mathbf{Q}, \mathbf{S}) - 1$，对所有 $i$ 成立。