题目描述

Alice 和 Bob 将要玩一个名为二分搜索的游戏。游戏在一个由 $2^{\mathbf{L}}$ 个格子组成的单行棋盘上进行。每个格子中包含一个介于 1 到 $\mathbf{N}$ 之间的整数（包括 1 和 $\mathbf{N}$）。此外，还有编号为 1 到 $\mathbf{N}$ 的 $\mathbf{N}$ 张卡片。在游戏开始前，裁判会以 $\mathbf{M}^{\mathbf{N}}$ 种可能的分配方式之一，在每张卡片上写下一个介于 1 到 $\mathbf{M}$ 之间的整数（包括 1 和 $\mathbf{M}$）。Alice 和 Bob 在游戏开始前知道棋盘上每个格子的整数以及每张卡片上的数字。

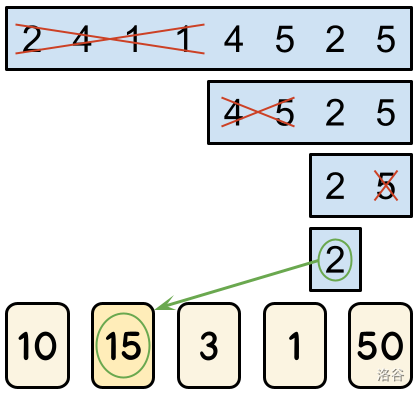
游戏以轮流进行的方式展开，Alice 先手。总共有 $\mathbf{L}$ 轮，这意味着 Alice 会进行 $\lceil \mathbf{L}/2 \rceil$ 轮，而 Bob 会进行 $\lfloor \mathbf{L}/2 \rfloor$ 轮。在每一轮中，玩家可以选择消除剩余格子中最左侧的一半或最右侧的一半。例如，假设棋盘上的数字为 $[2, 4, 1, 1, 4, 5, 2, 5]$。在 Alice 的第一轮中，她必须选择消除其中一半，留下 $[2, 4, 1, 1]$ 或 $[4, 5, 2, 5]$。如果她选择消除最左侧的一半并留下 $[4, 5, 2, 5]$，那么 Bob 必须在下一轮中选择留下 $[4, 5]$ 或 $[2, 5]$。如果他选择留下 $[2, 5]$，那么在最后一轮中，Alice 将需要在 $[2]$ 和 $[5]$ 之间做出选择。

游戏结束时，他们查看唯一剩下的格子中的数字 $X$。游戏的分数就是编号为 $X$ 的卡片上所写的整数。在上述例子中，如果 Alice 在最后一轮中消除 $[5]$ 并留下 $[2]$，那么游戏的分数就是裁判在编号为 2 的卡片上写的数字。

Alice 会采取最优策略以最大化游戏分数，而 Bob 则会采取最优策略以最小化分数。他们在一个固定的棋盘上进行游戏，棋盘上的格子中分别写着整数 $\mathbf{A}_1$, $\mathbf{A}_2$, …, $\mathbf{A}_{2^{\mathbf{L}}}$。为了确保最大限度的公平性，他们会进行 $\mathbf{M}^{\mathbf{N}}$ 局游戏，每局游戏中裁判会以不同的方式在卡片上写数字。这意味着对于每一种可能的卡片分配方式，Alice 和 Bob 都会恰好进行一局游戏。给定游戏参数和固定的棋盘内容，请计算所有游戏的分数之和。由于输出可能是一个非常大的数字，我们只要求你输出结果对质数 $10^9 + 7$（即 $1000000007$）取模后的余数。

输入格式

输入的第一行包含测试用例的数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例包含恰好两行。第一行包含三个整数 $\mathbf{N}$、$\mathbf{M}$ 和 $\mathbf{L}$。第二行包含 $2^{\mathbf{L}}$ 个整数 $\mathbf{A}_1$, $\mathbf{A}_2$, …, $\mathbf{A}_{2^{\mathbf{L}}}$，其中 $\mathbf{A}_i$ 表示棋盘上从左数第 $i$ 个格子中的整数。

输出格式

对于每个测试用例，输出一行 Case #x: y，其中 $x$ 是测试用例编号（从 1 开始），$y$ 是所有 $\mathbf{M}^{\mathbf{N}}$ 局游戏的分数之和模 $10^9 + 7$（即 $1000000007$）后的结果。

输入输出样例 #1

输入 #1

3
2 2 2
2 1 1 1
4 3 2
3 1 1 4
5 100 3
2 4 1 1 4 5 2 5

输出 #1

Case #1: 6
Case #2: 144
Case #3: 991661422

说明/提示

样例解释

在样例 #1 中，有 4 种卡片分配方式：$[1, 1]$、$[1, 2]$、$[2, 1]$ 和 $[2, 2]$。在前两种分配方式中，无论 Alice 在首轮如何选择，Bob 总能使得最终剩下的格子中的数字为 1，而卡片 1 上的数字为 1，因此这两局游戏的分数均为 1。在后两种分配方式中，Alice 可以通过在首轮消除棋盘最左侧的一半，留下 $[1, 1]$，此时 Bob 别无选择，只能留下 $[1]$。由于在这两种分配方式中卡片 1 上的数字为 2，因此这两局游戏的分数均为 2。所有分数的总和为 $1 + 1 + 2 + 2 = 6$。

数据范围

• $1 \leq \text{T} \leq 12$。
• $1 \leq \text{L} \leq 5$。
• 对于所有 $i$，满足 $1 \leq \text{A}_i \leq \text{N}$。

测试集 1（9 分，可见判定结果）

• $1 \leq \text{N} \leq 8$。
• $1 \leq \text{M} \leq 100$。

测试集 2（26 分，隐藏判定结果）

• $1 \leq \text{N} \leq 32$。
• $1 \leq \text{M} \leq 10^9$。