DIVCNT2 - Counting Divisors (square)

题面翻译

$\sigma_0(i)$ 表示$i$ 的约数个数

求$S_2(n)=\sum_{i=1}^n\sigma_0(i^2)$

多测。

答案对$2^{64}$取模。

数据范围：

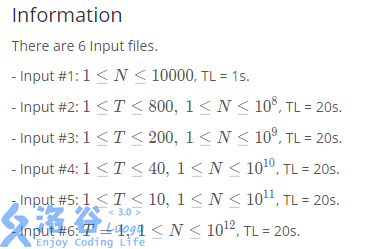
Translated by @Kelin

题目描述

Let $\sigma_0(n)$ be the number of positive divisors of $n$ .

For example, $\sigma_0(1) = 1$ , $\sigma_0(2) = 2$ and $\sigma_0(6) = 4$ .

Let

Given $N$ , find $S_2(N)$ .

输入格式

First line contains $T$ ( $1 \le T \le 10000$ ), the number of test cases.

Each of the next $T$ lines contains a single integer $N$ . ( $1 \le N \le 10^{12}$ )

输出格式

For each number $N$ , output a single line containing $S_2(N)$ .

样例 #1

样例输入 #1

5
1
2
3
10
100

样例输出 #1

1
4
7
48
1194