题目描述

译自 JOI Open 2014 Day2 T2「ピンボール / Pinball」

Alice 喜欢一款叫做弹球的视频游戏。弹球的规则如下。

弹球的板子是一个有 $M+2$ 行和 $N$ 列的方格网。板子的第一行是板子的顶部，第 $M+2$ 行是板子的底部。第 $i$ 行和第 $j$ 列的方格用 $(i, j)$ 表示。

一个球会出现在板子第一行的某个方格上，然后垂直地向板子的底部落下。也就是说，如果一个球出现在方格 $(1, i)\ (1 \leq i \leq N)$ 上，它会经过 $(j, i)$ $(2 \leq j \leq M+1)$，最后到达底部的 $(M+2, i)$。Alice 成功地击回球时会得到分数。

有一天，Alice 发现很难击回球，因为一个球可能到达底部的任何方格。Alice 决定在板子上适当地放置一些以下的装置，使得底部只有一个方格是球可能到达的。

有 $M$ 个装置，从 $1$ 到 $M$ 编号。每个装置都平行于板子的行。装置 $i$ $(1 \leq i \leq M)$ 占据了从 $(i+1, A_{i})$ 到 $(i+1, B_{i})$ 的方格。因此，它总共覆盖了 $B_{i}-A_{i}+1$ 个方格。当一个球到达这个装置上的某个方格时，球会被传送到方格 $(i+1, C_{i})\ (A_{i} \leq C_{i} \leq B_{i})$。之后，传送后的球会沿着列 $C_{i}$ 垂直移动。一个装置不会与一个球碰撞超过一次。

她需要在游戏中支付 $D_{i}$ 日元来把装置 $i\ (1 \leq i \leq M)$ 放在板子上。她会选择一些装置放在板子上，使得底部只有一个方格是球可能到达的。她想通过合理地放置装置来最小化总花费。

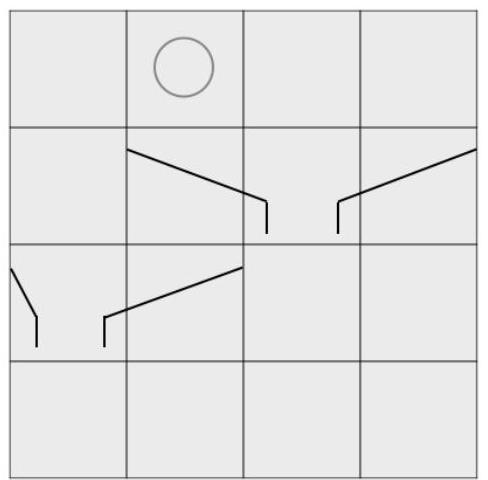
这是 $M=2, N=4$ 的弹球板子的一个例子。一个球出现在第一行的方格 $(1,2)$ 上。然后，球会移动到 $(2,2)$，并被装置 $1$ 传送到 $(2,3)$。它最后到达底部的方格 $(4,3)$。

给定板子的大小和装置的信息，你需要编写一个程序来计算当底部只有一个方格是球可到达的时，放置装置的最小总花费。

输入格式

第一行包含两个用空格分隔的整数 $M, N$，表示板子有 $M+2$ 行和 $N$ 列，装置的数量是 $M$。

接下来的 $M$ 行中的第 $i\ (1 \leq i \leq M)$ 行包含四个用空格分隔的整数 $A_{i}, B_{i}, C_{i}, D_{i}$，表示装置 $i$ 占据了从 $(i+1, A_{i})$ 到 $(i+1, B_{i})$ 的方格。装置 $i$ 总共覆盖了 $B_{i}-A_{i}+1$ 个方格。装置 $i$ 会把到达这些方格中的一个的球传送到方格 $(i+1, C_{i})$。放置装置 $i$ 的花费是 $D_{i}$ 日元。

输出格式

输出一行包含一个整数，表示放置装置的最小总花费，使得底部只有一个方格是球可能到达的。如果不可能放置装置满足这些条件，输出 $-1$。

5 6
2 4 3 5
1 2 2 8
3 6 5 2
4 6 4 7
2 4 3 10

25

3 5
2 4 3 10
1 3 1 20
2 5 4 30

-1

数据范围与提示

对于所有输入数据，满足：

• $1 \leq M \leq 10^5$
• $2 \leq N \leq 10^9$
• $1 \leq A_{i} \leq C_{i} \leq B_{i} \leq N\ (1 \leq i \leq M)$
• $1 \leq D_{i} \leq 10^9\ (1 \leq i \leq M)$

详细子任务附加限制及分值如下表所示。