题目描述

题目译自 BalticOI 2023 Day2「Mineral deposits」

你为一家地外采矿公司处理信号，你的飞船正在接近一颗小行星。初步扫描显示，小行星上存在 $k$ 个矿床，但其确切位置尚不清楚。

小行星表面可以看作是一个整数坐标网格。每个矿床都位于未知的整数坐标上，第 $i$ 个矿床的坐标为 $(x_i , y_i)$，其中 $-b \le x_i \le b$，$-b \le y_i \le b$，整数 $b$ 与初始扫描的区域大小相对应。

为了确定矿床的精确位置，您可以向小行星表面发送探测器组。一组探测器由数个探测器一起组成。

假设你发送了一组 $d$ 个探测器，对于 $1\le j\le d$，第 $j$ 个探测器发送到坐标 $(s_j, t_j)$。当探测器到达指定位置时，它会确定到这 $k$ 个矿床的每个的曼哈顿距离，并把这些距离发回给飞船。所有数据包会同时到达，并且不可能确定哪个探测器发回的距离是什么。因此这组探测器会返回 $k\cdot d$ 个整数距离

$$|x_i-s_j|+|y_i-t_j| \quad \forall i\in\{1,\ldots,k\},j\in\{1,\ldots,d\} $$

你需要最小化发送到小行星表面的探测器组数。

交互过程

这是一道交互题。交互开始于你读入一行三个整数 $b,k$ 和 $w$：网格的边界 $b$，$k$ 个矿床和最多可以发送的探测器组数 $w$。

然后你可以询问最多 $w$ 次，每次表示一个探测器组。一个询问由一个 $\texttt{?}$ 和紧接着的 $2d$ 个由空格分隔的整数组成，如 $\texttt{?}\ s_1\ t_1\ \cdots\ s_d\ t_d$，其中 $d$ 为这组探测器中包含的探测器数，必须满足 $1\le d\le 2000$。$(s_i,t_i)$ 是第 $i$ 个探测器的坐标，必须满足 $-10^8\le s_i\le 10^8$ 且 $-10^8\le t_i\le 10^8$。回答是一行 $k\cdot d$ 个非递减顺序给出的整数：表示所有矿床和探测器对之间的曼哈顿距离。所有探测器组中包含的探测器数不能超过 $2\cdot 10^4$。

交互结束于你输出一行由 $\texttt{!}$ 和紧接着的 $k$ 个点 $x_1,y_1,x_2,y_2,\ldots,x_k,y_k$，点坐标用空格分隔。这必须是你输出的最后一行。

特别提示：对于每行输出，你必须输出换行（\n），并刷新缓冲区。

如果你输出了所有矿床的位置，那么你的提交会被认为是正确的。你可以以任意顺序输出。

限制和计分

数据满足 $1\le b\le 10^8,1\le k\le 20$ 和 $2\le w\le 10^4$。

你的提交将在一些子任务中进行测试，每个子任务都有一定的分数。每个子任务都包含一些测试用例。要获得子任务的分数，你需要解决子任务中的所有测试用例。你的最终得分将是单次提交的最高分。

子任务编号	附加限制	分值
$1$	$k=1,w=10^4$	$9$
$2$	$w\ge 500$	$19$
$3$	$w\ge 210$	$11$
$4$	$w\ge 130$	$7$
$5$	$w\ge 3,b\le 10^4$	$20$
$6$	$w\ge 3,b\le 10^7$	$15$
$7$	无附加限制	$19$

样例交互

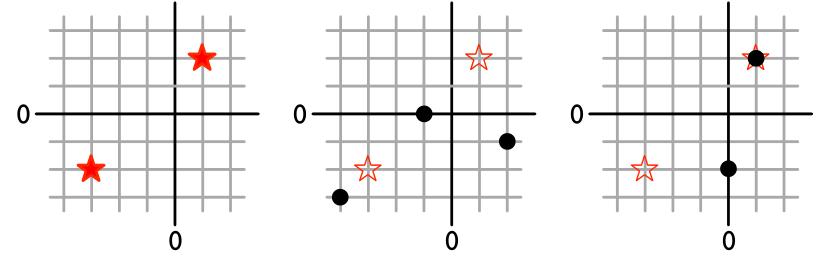
在这组样例中，有 $k=2$ 个矿床位于 $(1,2)$ 和 $(-3,-2)$，用红星标出。在第一组探测器中，你可以发送 $d=3$ 个探测器到 $(-4,-3),(-1,0)$ 和 $(2,-1)$，用黑点标出。这组探测器会返回 $6$ 个距离：

$$2,4,4,4,6,10.$$

对于下一组探测器，你可以发送 $d=2$ 个探测器到 $(1,2)$ 和 $(0,-2)$。这组探测器会返回 $4$ 个距离：

$$0,3,5,8.$$

读	写
4 2 10
	? -4 -3 -1 0 2 -1
2 4 4 4 6 10
	? 1 2 0 -2
0 3 5 8
	! 1 2 -3 -2