题目描述

题目译自 BalticOI 2024 Day1「Portal」

你觉得欺骗你最好的朋友会很有趣，你把他放在一个无限网格的 $(0, 0)$ 单元格上。然后你的朋友会在这个网格上无限地移动，每次移动一步，并且总是移动到相邻的四个单元格之一。

网格上有 $N$ 个单元格包含一个传送门。一旦你的朋友踩到一个传送点，他就会瞬间传送到一个随机的传送点处（可能是他刚刚踩到的那个，也可能是不同的一个）。如果 $(0, 0)$ 单元格也有一个传送门，你的朋友一开始被放置在网格上时也会被传送。

作为这个恶作剧的一部分，你想让你的朋友完全不会发现有传送点的存在。你的朋友只能看到他当前所在单元格的颜色，所以你应该确保从你朋友的视角来看，单元格的颜色永远不会变化。特别是，如果你的朋友认为他已经进入过某个单元格（例如先向左移动，然后立即向右移动），他应该看到与第一次进入时相同的颜色。

注意：当你的朋友踩到传送点时，他会看到传送点所在单元格的颜色，以及他被传送到的单元格的颜色。因此，你需要将所有包含传送门的单元格染成相同的颜色，以避免传送时暴露。

一个简单的解决方案是将所有单元格染成相同的颜色。但是颜色很好！所以你想尽可能使用更多的颜色。

让我们考虑一个例子，其中传送门位于 $(1, 1),(1, 3)$ 和 $(3, 2)$ 单元格，你的朋友进行了以下一系列移动:向上、向右、向下、向左。

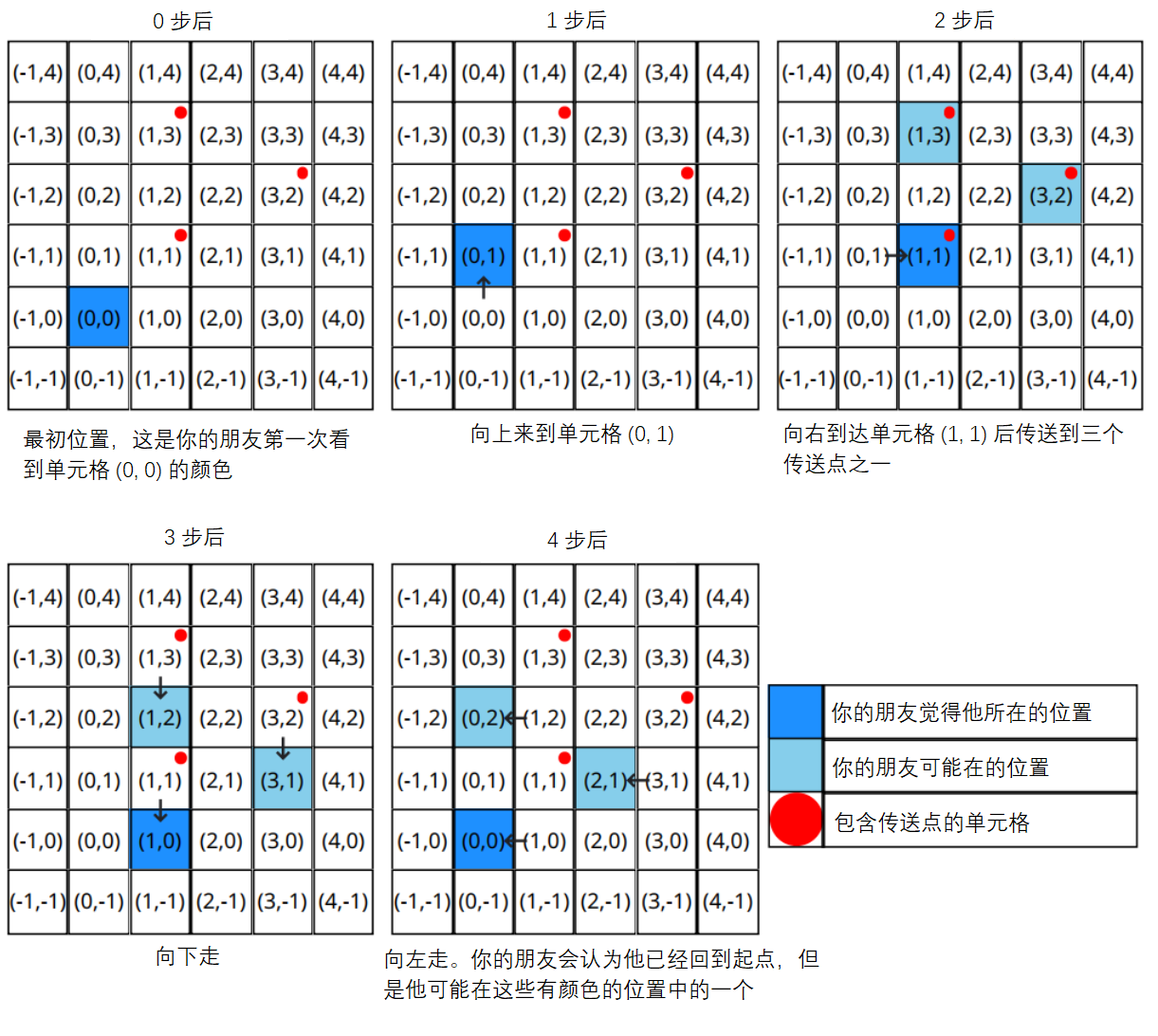
在一系列的移动之后，朋友会认为他又回到了起点单元格 $(0, 0)$，但实际上他也有可能到了 $(0, 2)$ 或 $(2, 1)$。他在开始时已经看到了单元格 $(0, 0)$ 的颜色，所以如果他现在看到了不同的颜色，他就会意识到这里肯定有传送门。我们不希望发生这种情况，所以我们必须为这三个单元格选择相同的颜色。

没有任何一连串的移动会让你的朋友认为他最终到达了单元格 $(0, 0)$，而实际上他最终到达了单元格 $(1, 0)$，因此这些单元格可以安全地涂上不同的颜色。

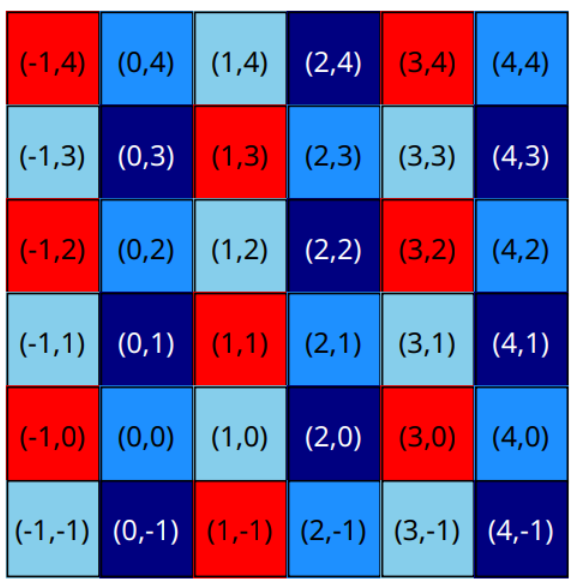
下面是上面例子中 $4$ 种颜色的着色。本例不可能使用超过 $4$ 种颜色。

我们再来看一个不同的例子，在单元格 $(0,0),(0,1),(1,0),(0,-1)$ 和 $(-1,0)$ 处都有传送点。假设你的朋友试图通过向右走一步然后向上走三步到达单元格 $(1,3)$。一种可能是，如果他在开始时和每一步之后都被传送到了单元格 $(0,0)$。如果你的朋友现在通过向下走三步，再向左走一步返回到他认为的单元格 $(0,0)$，并且在此过程中没有被传送离开他所到单元格，那么他最终会到达 $(-1,-3)$。而你的朋友会认为他们第二次来到了单元格 $(0,0)$，并希望看到相同的颜色。因此，你需要给 $(-1,-3)$ 和 $(0,0)$ 涂上相同的颜色。

请注意，我们最初选择的单元格 $(1,3)$ 并没有什么特别之处。同样，你也可以证明其他单元格必须与 $(0,0)$ 颜色相同。

在确保你的朋友不会发现有传送点存在的前提下，计算出你可以使用的颜色的最大数量。

输入格式

第一行包含一个整数 $N$，表示传送点个数。

接下来 $N$ 行每行两个整数。第 $i$ 行包含 $x_i$ 和 $y_i$，表示单元格 $(x_i,y_i)$ 处有一个传送点。

输出格式

输出一个整数，表示在你的朋友不会发现有传送点存在的情况下可以使用的最大颜色数，如果可以使用无限多种颜色，则输出 $-1$。

3
1 1
1 3
3 2

4

5
0 0
1 0
-1 0
0 1
0 -1

1

1
1 -1

-1

数据范围与提示

对于所有数据，满足：

• $1\le N\le 10^5$
• $-10^6\le x_i,y_i\le 10^6$（对于所有 $1\le i\le N$）
• 没有两个传送点位于同一单元格

详细子任务附加限制及分值如下表所示。

子任务编号	附加限制	分值
$1$	$N\le 2$	$1$
$2$	$N\le 3$	$10$
$3$	对于所有整数 $x_1,x_2,y_1,y_2$：如果 $(x_1,y_1)$ 和 $(x_2,y_2)$ 处有传送点，那么 $(x_1,y_2)$ 处也有传送点
$4$	$N\le 100$ 且 $-100\le x_i,y_i\le 100$（对于 $1\le i\le N$）	$29$
$5$	$N\le 2000$	$15$
$6$	无附加限制	$35$