题目描述

杨柳国的地图可以抽象成一张 $n$ 个点 $m$ 条边的无向连通图，每条边等长。图上有 $k$ 个人，其中第 $i$ 个人住在点 $a_i$，每天都要去 $b_i$ 上班。他会选择一条长度最短的路径，如果有多条，则等概率随机一条。

小 G 想找一个点开便利店。具体来说，她定义了 $E_i(w)$ 表示第 $i$ 个人经过点 $w$ 的概率，你需要帮助她找出 $\sum^{k-1}_{i=0} E_i(w)$ 最大的点 $w$。如有多个，可输出任意一个。

题目描述

第一行，两个正整数 $n$ 和 $m$。

接下来 $m$ 行，每行两个整数 $u$ 和 $v$，表示一条边（节点编号从 $0$ 到 $n − 1$）。

接下来一行，一个正整数 $k$。

接下来 $k$ 行，每行两个整数 $a_i$ 和 $b_i$，表示第 $i$ 个人的起点和终点。

输出格式

一行，一个整数 $w$ 表示最佳便利店位置。

样例

样例 1

5 5
0 1
1 2
2 3
3 4
4 0
2
1 3
2 4

2 或 3

注意这里指的是 $2$ 或 $3$ 均可。

样例 2

5 4
0 1
1 2
2 3
3 4
3
0 2
1 3
2 4

2

样例 3

6 5
0 2
1 2
2 3
3 4
3 5
2
0 5
1 4

2 或 3

样例 4

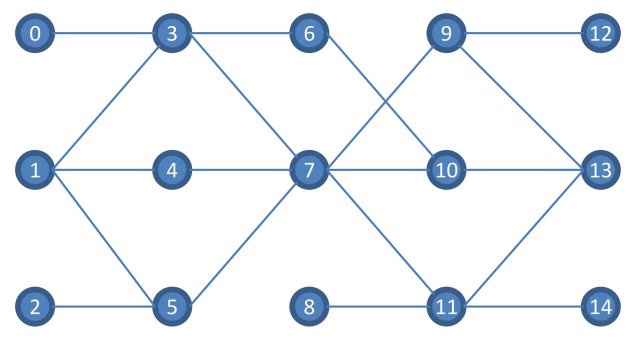
15 19
0 3
1 3
1 4
1 5
2 5
3 6
3 7
4 7
5 7
6 10
7 9
7 10
7 11
8 11
9 12
9 13
10 13
11 13
11 14
2
4 10
3 8

7

数据范围

• 子任务 $1$，分值 $4$ 分，保证图是一条链，$n\le 10^3$，$m=n-1$，$k=1$。
• 子任务 $2$，分值 $5$ 分，保证图是一条树，$n\le 10^3$，$m=n-1$，$k=1$。
• 子任务 $3$，分值 $11$ 分，保证图是一条链，$n\le 10^3$，$m=n-1$，$k\le 200$。
• 子任务 $4$，分值 $18$ 分，保证图是一条树，$n\le 10^3$，$m=n-1$，$k\le 200$。
• 子任务 $5$，分值 $26$ 分，保证 $n\le 10^3$，$m\le 8\times 10^3$，$k\le 20$。
• 子任务 $6$，分值 $36$ 分，保证 $n\le 5\times 10^3$，$m\le 4\times 10^4$，$k\le 2\times 10^3$。

对所有数据，保证任意两点间最短路径数量不超过 $2^{15}$，注意本题需使用 double。