题目描述

给定一个长度为 $n$ 的木板，木板上有 $m$ 个标记点，距离木板左端点的距离分别为 $X_i$，现你需要在木板上放置一些不相交正方形，正方形需要满足：

• 正方形的边长为整数；

• 正方形底面需要紧贴木板；

• 正方形不能超出木板，正方形要将所有的木板覆盖；

• 标记点的位置不能是两个正方形的交界处。

下面是一些满足条件与不满足条件的例子：

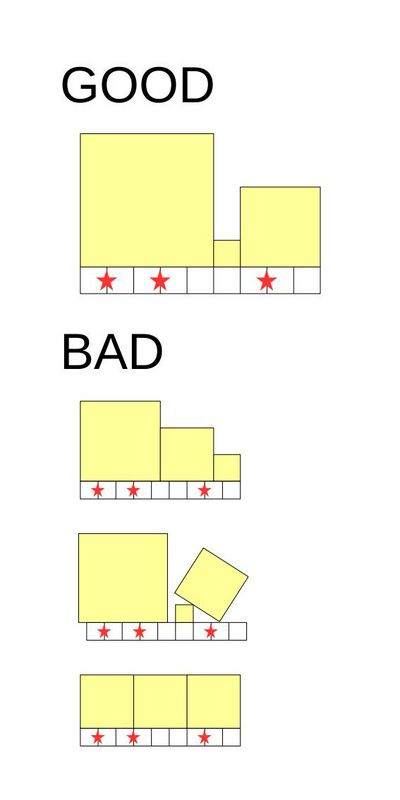
一种合法的正方形放置方案的贡献为所有正方形面积的乘积，也就是为 $\prod\limits_{i=1}^k a_i^2$ 为正方形的边长。

请你求出所有合法方案的贡献之和，答案对 $10^9+7$ 取模。

输入格式

第一行两个整数 $n,m$。

第二行 $m$ 个整数，表示 $x_1,x_2,\cdots,x_{m-1},x_m$。

输出格式

输出一个整数，表示答案对 $10^9+7$ 取模的结果。

样例

3 1
2

3 1
2

5 2
2 3

66

10 9
1 2 3 4 5 6 7 8 9

100

1000000000 0

693316425

数据范围

$1\le n \le 10^9$，$0\le m \le 10^5$。

$1\le x_1 < x*_2 < \cdots x_{m-1} < x_m \le n-1$。