树论（二）

Problem Description

Yoshinow又得到了一棵 $n$ 个结点的树，结点的标号为 $1$ 到 $n$ 内的整数，Yoshinow突发奇想：如果把树上的一条边删掉后， 一棵树会被划成两棵树 $T_1,T_2$，从 $T_1$ 的节点编号中选一个数 $x$，再从 $T_2$ 的结点编号中选一个数 $y$，$\textrm{gcd(x,y)}$ 最大能取到多少？ 因为Yoshinow非常好奇，所以他想对每条边都询问。 **形式化地说：**有一棵树 $G=(V,E)$, $V=\{1,2,\dots ,n\}$，$n-1$ 条边 $E=\{(u_1,v_1),\dots ,(u_{n-1},v_{n-1})\}$. 对每条边 $(u_i,v_i)(i=1,\dots,n-1)$，需要回答：将 $(u_i ,v_i)$ 删去后，原树 $G$ 会被分成不连通的两棵树 $G_1=(V_1,E_1),G_2=(V_2,E_2)$， 此时 $\max_{x\in V_1,y_\in V_2} \textrm{gcd(x,y)}$是多少

Input

第一行一个正整数 $T$，表示测试用例组数，$1\leq T\leq 10$. 接下来 $T$ 组数据，对每组数据：先输入一个正整数 $n$，表示树的点数， $2\leq n\leq 10^6$，接下来 $n-1$ 行，第 $i$ 行包括两个整数 $u_i,v_i$，表示树上的第 $i$ 条边为 $(u_i,v_i)$. 保证对所有测试用例，$\sum n\leq 5\times 10^6$.

Output

对每个测试用例，输出一行 $n-1$ 个整数，第 $i$ 个整数表示删除边 $(u_i,v_i)$ 后的答案。 注：在这题中你可能需要用到更大的栈空间，C++选手可以在main函数中加入如下代码，以防出现栈溢出的错误：

int main() {
int size(256<<20); //256M
__asm__ ( "movq %0, %%rsp\n"::"r"((char*)malloc(size)+size));
// YOUR CODE
//...
exit(0);
}

Sample Input

2
3
1 2
2 3
4
1 2
2 3
2 4

Sample Output

1 1
1 1 2

Hint

两个样例如下图所示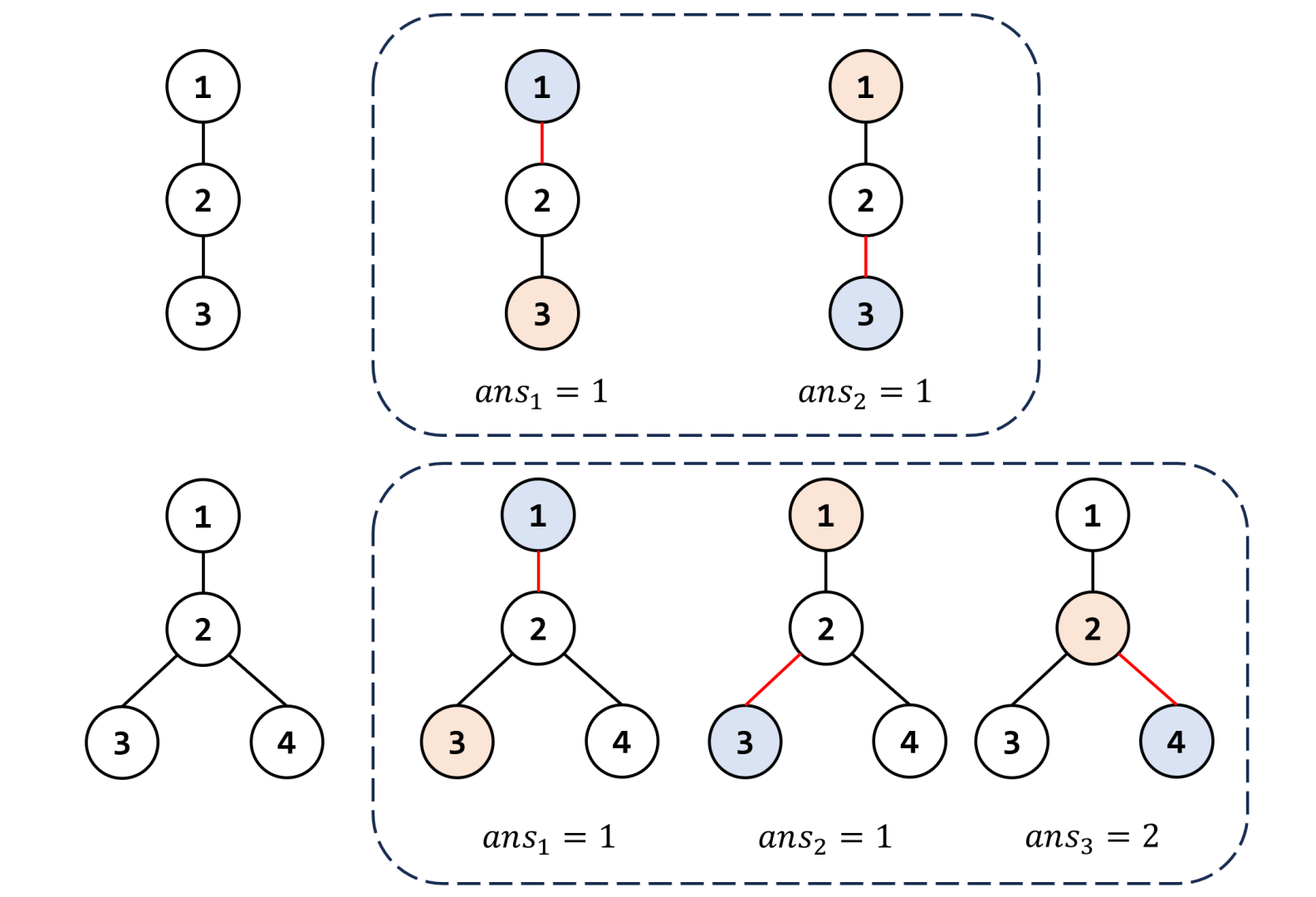： 红边表示询问的边，选取的点 $x,y$ 对应地用浅蓝色和橙色标注。在样例中，除了第二棵树的 $ans_3$ 以外，其他询问中的无序对 $\{x,y\}$ 的选取方式都不唯一。

Source

2024“钉耙编程”中国大学生算法设计超级联赛（5）