Minimal k-covering

题面翻译

题目大意

给你一张二分图 $G = (U, V, E)$ ， $U$ 是图的 $X$ 部， $V$ 是图的 $Y$ 部， $E$ 是边集，可能有重边。

我们称 $E$ 的某个子集 $\overline E$ 是 k-覆盖 的，当且仅当图 $\overline G = (U, V, \overline E)$ 的每个顶点至少连接了 $k$ 条边；若 $\overline E$ 是 k-覆盖 的且不存在元素个数比它更小的边集也是 k-覆盖 的，则称 $\overline E$ 是一个 最小k-覆盖 。

你的任务是对于所有 $k \in [0, minDegree]$ ，求出 最小k-覆盖，其中 $minDegree$ 是图 $G$ 的所有点度数的最小值。

输入格式

第一行输入三个整数 $n_1$ ， $n_2$ 和 $m$ （ $1 \le n_1, n_2 \le 2000$ ， $0 \le m \le 2000$ ），分别代表 $U$ 的点数， $V$ 的点数和边数。

接下来 $m$ 行每行两个整数 $u_i$ 和 $v_i$ ，表示第 $i$ 条边在 $U$ 中的端点为 $u_i$ ，在 $V$ 中的端点为 $v_i$ 。

输出格式

输出包含 $minDegree + 1$ 行，每行首先输出一个整数 $cnt_k$ ，表示 最小k-覆盖 的边集大小，紧接着输出 $cnt_k$ 个整数，表示属于 最小k-覆盖 的边的标号。边按输入顺序从 $1$ 开始标号。输出时不必按标号从小到大输出。

感谢@OrangeLee 提供的翻译

题目描述

You are given a bipartite graph $G=(U,V,E)$ , $U$ is the set of vertices of the first part, $V$ is the set of vertices of the second part and $E$ is the set of edges. There might be multiple edges.

Let's call some subset of its edges 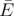$k$ -covering iff the graph 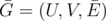has each of its vertices incident to at least $k$ edges. Minimal $k$ -covering is such a $k$ -covering that the size of the subset 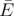is minimal possible.

Your task is to find minimal $k$ -covering for each 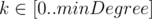, where $minDegree$ is the minimal degree of any vertex in graph $G$ .

输入格式

The first line contains three integers $n_{1}$ , $n_{2}$ and $m$ ( $1<=n_{1},n_{2}<=2000$ , $0<=m<=2000$ ) — the number of vertices in the first part, the number of vertices in the second part and the number of edges, respectively.

The $i$ -th of the next $m$ lines contain two integers $u_{i}$ and $v_{i}$ ( $1<=u_{i}<=n_{1},1<=v_{i}<=n_{2}$ ) — the description of the $i$ -th edge, $u_{i}$ is the index of the vertex in the first part and $v_{i}$ is the index of the vertex in the second part.

输出格式

For each 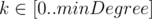print the subset of edges (minimal $k$ -covering) in separate line.

The first integer $cnt_{k}$ of the $k$ -th line is the number of edges in minimal $k$ -covering of the graph. Then $cnt_{k}$ integers follow — original indices of the edges which belong to the minimal $k$ -covering, these indices should be pairwise distinct. Edges are numbered $1$ through $m$ in order they are given in the input.

样例 #1

样例输入 #1

3 3 7
1 2
2 3
1 3
3 2
3 3
2 1
2 1

样例输出 #1

0 
3 3 7 4 
6 1 3 6 7 4 5

样例 #2

样例输入 #2

1 1 5
1 1
1 1
1 1
1 1
1 1

样例输出 #2

0 
1 5 
2 4 5 
3 3 4 5 
4 2 3 4 5 
5 1 2 3 4 5