Rectangle Painting 2

题面翻译

有一个$n*n$的网格，网格中有一些点是黑的，其他点都是白的。你每次可以花费$\min(h,w)$的代价把一个$h*w$的矩形区域变白。求把所有黑格变白的最小代价。

输入格式

第一行2个整数$n$,$m$（$1\le n \le 10^9,0\le m\le 50$）,分别代表正方形网格的大小和黑色矩形的数量。

接下来$m$行,每行$4$个整数$x_{i1},y_{i1},x_{i2},y_{i2}$（$1\le x_{i1}\le x_{i2}\le n,1\le y_{i1}\le y_{i2}\le n$）,分别代表黑色矩形左下角的格子和右上角的格子。（显然，黑色矩形里的格子都是黑的。）

黑色矩形可能相交。

输出格式

一个整数：把所有格子变白的最小代价。

题目描述

There is a square grid of size $n \times n$ . Some cells are colored in black, all others are colored in white. In one operation you can select some rectangle and color all its cells in white. It costs $\min(h, w)$ to color a rectangle of size $h \times w$ . You are to make all cells white for minimum total cost.

The square is large, so we give it to you in a compressed way. The set of black cells is the union of $m$ rectangles.

输入格式

The first line contains two integers $n$ and $m$ ( $1 \le n \le 10^{9}$ , $0 \le m \le 50$ ) — the size of the square grid and the number of black rectangles.

Each of the next $m$ lines contains 4 integers $x_{i1}$ $y_{i1}$ $x_{i2}$ $y_{i2}$ ( $1 \le x_{i1} \le x_{i2} \le n$ , $1 \le y_{i1} \le y_{i2} \le n$ ) — the coordinates of the bottom-left and the top-right corner cells of the $i$ -th black rectangle.

The rectangles may intersect.

输出格式

Print a single integer — the minimum total cost of painting the whole square in white.

样例 #1

样例输入 #1

10 2
4 1 5 10
1 4 10 5

样例输出 #1

4

样例 #2

样例输入 #2

7 6
2 1 2 1
4 2 4 3
2 5 2 5
2 3 5 3
1 2 1 2
3 2 5 3

样例输出 #2

3

提示

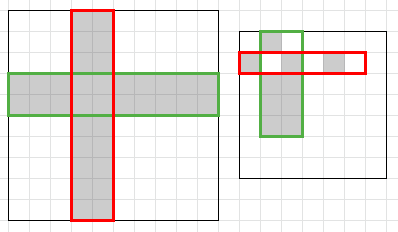
The examples and some of optimal solutions are shown on the pictures below.