The Child and Binary Tree

题面翻译

我们的小朋友很喜欢计算机科学，而且尤其喜欢二叉树。 考虑一个含有 $n$ 个互异正整数的序列 $c_1,c_2\cdots,c_n$。如果一棵带点权的有根二叉树满足其所有顶点的权值都在集合 $\{c_1,c_2,\cdots,c_n\}$ 中，我们的小朋友就会将其称作神犇的。

并且他认为，一棵带点权的树的权值，是其所有顶点权值的总和。

给出一个整数 $m$，你能对于任意的 $1\leq s\leq m$ 计算出权值为 $s$ 的神犇二叉树的个数吗？请参照样例以更好的理解什么样的两棵二叉树会被视为不同的。 我们只需要知道答案关于 $998244353$ 取模后的值。

输入第一行有 $2$ 个整数 $n,m$ $(1\leq n,m\leq 10^5)$。 第二行有 $n$ 个用空格隔开的互异的整数 $c_1,c_2\cdots,c_n$ $(1\le c_i\le10^5)$。

输出 $m$ 行，每行有一个整数。第 $i$ 行应当含有权值恰为 $i$ 的神犇二叉树的总数。请输出答案关于 $998244353$ 取模的结果。

题目描述

Our child likes computer science very much, especially he likes binary trees.

Consider the sequence of $n$ distinct positive integers: $c_{1},c_{2},...,c_{n}$ . The child calls a vertex-weighted rooted binary tree good if and only if for every vertex $v$ , the weight of $v$ is in the set ${c_{1},c_{2},...,c_{n}}$ . Also our child thinks that the weight of a vertex-weighted tree is the sum of all vertices' weights.

Given an integer $m$ , can you for all $s$ $(1<=s<=m)$ calculate the number of good vertex-weighted rooted binary trees with weight $s$ ? Please, check the samples for better understanding what trees are considered different.

We only want to know the answer modulo $998244353$ ( $7×17×2^{23}+1$ , a prime number).

输入格式

The first line contains two integers $n,m$ $(1<=n<=10^{5}; 1<=m<=10^{5})$ . The second line contains $n$ space-separated pairwise distinct integers $c_{1},c_{2},...,c_{n}$ . $(1<=c_{i}<=10^{5})$ .

输出格式

Print $m$ lines, each line containing a single integer. The $i$ -th line must contain the number of good vertex-weighted rooted binary trees whose weight exactly equal to $i$ . Print the answers modulo $998244353$ ( $7×17×2^{23}+1$ , a prime number).

样例 #1

样例输入 #1

2 3
1 2

样例输出 #1

1
3
9

样例 #2

样例输入 #2

3 10
9 4 3

样例输出 #2

0
0
1
1
0
2
4
2
6
15

样例 #3

样例输入 #3

5 10
13 10 6 4 15

样例输出 #3

0
0
0
1
0
1
0
2
0
5

提示

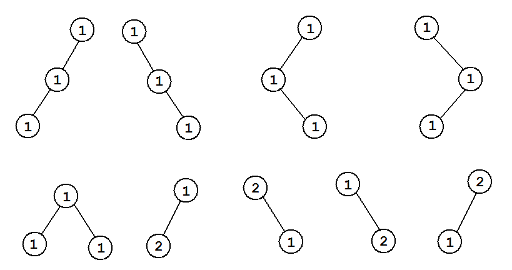
In the first example, there are $9$ good vertex-weighted rooted binary trees whose weight exactly equal to $3$ :